SONAR-INFO-p58
Dei segnali e del rumore 1)Generalità
NOTE : 2)Sul fenomeno e sui diagrammi del rumore del mare - dal lavoro di Knudsen- . 3)Sulla legge relativa all'attenuazione del segnale per assorbimento -Equazione di Thorp- 4)Simulazione di verifica sul campo -primo- 5)Simulazione di verifica sul campo -secondo- 6)Sull'equalizzazione del rumore del mare 7)Simulazione di verifica sul campo con equalizzazione -terzo- 8)Appendice - sul rumore elettronico dei preampificatori idrofonici-
Nei paragrafi precedenti abbiamo assunto che l'amplificatore di misura (am), riportato nelle figure 3 e 4,
fosse un dispositivo ideale privo di rumore proprio.
Ricezione sonar a larga banda
Sul rumore del mare e dei segnali si è trattato in termini discorsivi su p2(cap. 7-8-9) dissertando su gli effetti
che il primo provoca sui secondi penalizzando la scoperta sonar.
E' di notevole interesse tecnico esaminare numericamente gli argomenti citati che sono alla base
di qualsiasi considerazione di previsione di portate e di progetto del sonar.
Per affrontare la problematica si evidenziano numericamente i fenomeni che governano, sia il rumore
del mare, sia l'attenuazione per assorbimento dei raggi acustici, temi che saranno oggetto,
rispettivamente, dei paragrafi 2 e 3.
Quanto sopra sarà fatto con l'aiuto di un circuito di simulazione che rende tangibile il percorso
concettuale da seguire e nel presupposto che la propagazione non sia anomala.
In appendice tratteremo del rumore elettronico dei preamplificatori idrofonici.
(nella pagina tutti i valori logaritmici saranno arrotondati entro 1 dB )
(con il simbolo Hz* s'intende radice di Hz)
Quando si parla di rumore del mare si deve fare riferimento all'andamento dell'insieme
di curve tracciate in figura 1.

Queste curve indicano come varia la pressione acustica generata dal moto ondoso del mare in funzione dei
due parametri fondamentali che caratterizzano la fisica del fenomeno:
- parametro 1 -
La pressione acustica generata dipende dallo stato del mare (SS) secondo la tabella a colori di figura 1.
- parametro 2 -
La pressione acustica generata dal moto ondoso dipende dalla frequenza secondo l'andamento delle
rette riportate in figura 1.
La citata figura mostra 6 segmenti di retta diversamente colorati in dipendenza del valore dello
stato del mare (SS ) ad esse attribuito.
Le ascisse indicano, in scala logaritmica a 3 decadi, il campo delle frequenze generate dal moto ondoso; è coperto
un intervallo di valori che si estende da 100 Hz a 100 KHz.
Sulle ordinate, in scala lineare, sono indicati i livelli di pressione acustica del rumore espressi
in dB/microPa/Hz*, in un intervallo esteso da 0 dB a + 100 dB con 20 divisioni da 5dB/div.
La pendenza delle rette è di -5 dB/ottava con il crescere della frequenza; ciò evidenzia come il
livello del rumore del mare sia molto più elevato alle frequenze basse.
Ciascun segmento di retta, per i diversi stati del mare, è calcolabile dalla seguente espressione approssimata:
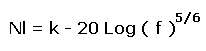 in dB/microPa/Hz* ; con f in KHz
in dB/microPa/Hz* ; con f in KHz
dove la variabile k dipende dallo stato del mare secondo la tabella:
ss = 0 ; K = 44
ss = 1/2 ; K = 51
ss = 1 ; K = 55
ss = 2 ; K = 62
ss = 4 ; K = 67
ss = 6 ; K = 71
L'utilizzo del diagramma nel caso si debba fare un computo di previsione in una data condizione
ambientale richiede l'assunzione di tre variabili; ad esempio:
1) lo stato del mare ( SS = 2 )
2) la frequenza centrale della banda da valutare ( f = 10 KHz )
3) la banda di frequenza entro la quale si valuta il rumore ( BW = 1000 Hz )
Per i due dati sopra esposti (SS = 2) -retta blu- ed f = 10 Khz , dalla figura 1 abbiamo:
livello di pressione pari a + 45 dB / microPa / Hz*
L'utilizzo del terzo dato ci consente di quantizzare il livello effettivo
della pressione di rumore PBW nella banda sopra definita:
PBW = + 45 dB/microPa/Hz* + 10 Log BW = + 45 dB/microPa/Hz* + 10 Log 1000 = + 75 dB/microPa/BW
Una formula generale per il calcolo dell'attenuazione delle onde acustiche per assorbimento del mezzo
è indicata come equazione di Thorp; l'equazione sotto riportata mostra l'entità dell'attenuazione (alfa),
espressa in dB / Km, in funzione della frequenza :
alfa = ((0.1 x f²) / (1 + f²)) + ((40 x f²) / (4100 + f²)) + 2.75 x f² / 10000
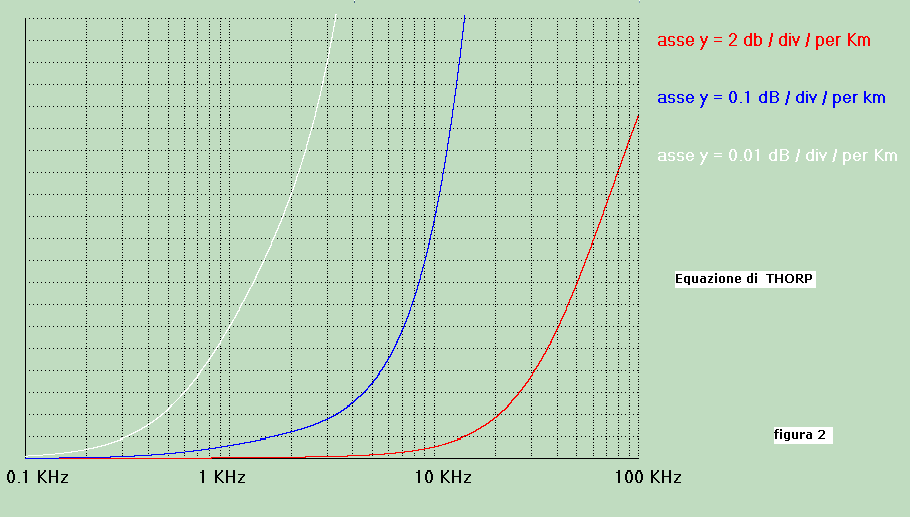
La funzione alfa è tracciata in figura 2, per tre diverse scale delle ordinate, nel campo di frequenza
compreso tra 100 Hz e 100 KHz.
Le scale delle ordinate, 2 dB/div/Km; 0.1 dB/div/Km; 0.01 dB/div/Km sono state inserite per poter
valutare quei tratti di curva relativi alle frequenze più basse per le quali l'attenuazione è piccola.
L'utilizzo del diagramma nel caso si debba fare un computo di previsione in una data condizione
ambientale richiede l'assunzione di due variabili; ad esempio:
1) la frequenza dell'onda acustica della sorgente ( f = 10000 Hz )
2) la distanza del percrso tra la sorgente acustica è il ricevitore ( D = 20 Km )
Per il primo dei due dati sopra esposti, f = 10000 Hz, dalla figura 2 (curva blu) abbiamo:
alfa = 11 div x 0.1 dB/div/Km = 1.1 dB/Km
L'utilizzo del secondo dato ci consente di quantizzare il valore totale dell'attenuazione
per assorbimento nel percorre D = 20 Km:
Atten.totale = alfa x D = 1.1 dB/Km x 20 Km = 22 dB
Per illustrare la tecnica di manipolazione dei dati sono utili una serie di
simulazioni sul campo simili alla seguente:
Nell'ipotesi di verificare i dati di previsione computati nell'esempio di par. 2) si
prende in esame il semplice circuito di figura 3:
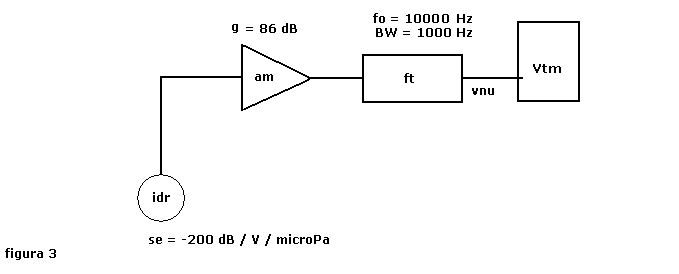
In esso s'individuano i seguenti componenti:
- idr idrofono omnidirezionale (immerso nella zona di misura), sensibilità: se = -200 dB / v / microPa
- am amplificatore ideale con rumore proprio nullo;
guadagno: g = 86 db costante in banda 100Hz-15000Hz
- ft filtro di banda: fo = 10000 Hz; banda BW = 1000 Hz ( 9500 Hz - 10500 Hz); attenuazione d'inserzione at = 6 dB
- vtm voltmetro in c.a. a vero valore efficace
La tensione di rumore vnu dovuta al mare, per ss = 2 computato in 2), misurata in uscita dal filtro sarà:
v1nu = PBW + se + g - at = +75 dB/microPa/BW - 200 dB/volt/microPa + 86 dB - 6 dB =
= -45 dB/V = 5.6 mV eff .
Supponiamo ora di dover simulare la ricezione di segnali idrofonici in un sonar a banda larga,
ad esempio tra 100 Hz e 10000 Hz ;
in tal caso il filtro ft del simulatore di figura 3 deve avere una larghezza di banda da 100 Hz a 10000 Hz.
Per calcolare la v2nu con la nuova banda si deve rivalutare, per essa, il rumore del mare (SS = 2) come
segue:
- si valuta la frequenza centrale della banda secondo la media geometrica degli estremi:
f = ( 100 Hz x 10000 Hz)½ = 1000 Hz
- in figura 1 (retta blu) per f = 1000 Hz si ha : + 62 dB/microPa/Hz*
- il rumore complessivo in banda 100-10000 Hz è dato da:
PBW = + 62 dB/microPa/Hz* + 10 Log( 10000 Hz - 100 Hz) = 102 dB/microPa/BW
La v2nu all'uscita del nuovo filtro di figura 3 sarà:
v2nu = PBW + se + g - at = +102 dB/microPa/BW - 200 dB/volt/microPa + 86 dB - 6 dB =
= -18 dB/V = 126 mV eff.
Il valore di v2nu ora calcolato sarà alla base delle considerazioni del successivo paragrafo
relativo al rapporto s/n all'uscita del filtro.
Al fine di studiare l'andamento del rapporto s/n all'uscita del filtro in presenza
di due diversi segnali idrofonici si impiega ancora il circuito di simulazione di figura 3 (banda 100 - 1000 Hz).
Ipotizziamo la ricezione, non simultanea, di due segnali idrofonici, s1 ed s2,
emessi da sorgenti acustiche diverse alla distanza di D = 20 Km da idr; siano Ls1 e Ls2 le
pressioni generate in banda BW1 e BW2:
-Ls1 = + 150 dB/microPa/BW1 a 300 Hz: BW1 = 200 Hz
-Ls2 = + 150 dB/microPa/BW2 a 9000 Hz: BW2 = 200 Hz
Ls1 e Ls2 subiranno un'attenuazione uguale per divergenza sferico-cilidrica di:
att = 60 dB + 10 Log 20 Km = 73 dB
Ls1 subirà un'attenuazione per assorbimento (vedi curva bianca figura2) pari a:
atas1 = 1 div x 0.01 dB/div x 20 Km = 0.2 dB ( si legga 0 dB)
Ls2 subirà un'attenuazione per assorbimento (vedi curva blu figura2) pari a:
atas2 = 9 div x 0.1 dB/div x 20 Km = 18 dB
Concludendo : Ls1 subirà un'attenuazione totale di 73 dB e Ls2 di 91 dB ; quindi
s1 colpirà il trasduttore con un livello di pressione :
Ps1 = 150 dB/microPa/BW1 - 73 dB = 77 dB/microPa/BW1
s2 colpirà il trasduttore con un livello di pressione :
Ps2 = 150 dB/microPa/BW1 - 92 dB = 58 dB/microPa/BW2
La tensione in uscita dal filtro di figura 3 sarà:
per s1: vns1 = Ps1 + se + g - at = +77 dB/microPa/BW - 200 dB/v/microPa + 86 dB - 6 dB =
= - 43 dB / volt = 7 mv eff
per S2: vns2 = Ps2 + se + g - at = +58 dB/microPa/BW - 200 dB/v/microPa + 86 dB - 6 dB =
= - 62 dB / volt = 0.8 mv eff
Da questi dati risultano i rapporti segnale/disturbo (r1; r2) tra vns1, vns2 e il rumore del
mare v2nu all'uscita del filtro:
r1 = vns1/v2nu = 7 mv eff / 126 mv eff : (s/n)dB = -25 dB
r2 = vns2/v2nu = 0.8 mv eff / 126 mv eff: (s/n)dB = - 44 dB
Il valore di r2 è peggiore di r1 di ben 19 dB, cosa da attribuire alla marcata attenuazione
per assorbimento di s2.
Generalmente quando la banda di ricezione del sonar è molto estesa si impiega un artificio
tecnico indicato come "equalizzazione del rumore del mare"; detto metodo consente di abbattere le
frequenze più basse del rumore del mare che, dato il loro elevato livello sotto i 100 Hz, possono
provocare disturbi sensibili alla ricezione.
L'equalizzazione riducendo lo spettro del disturbo alle frequenze basse riduce anche il livello
dei segnali idrofonici di BF che però, data la loro irrilevante attenuazione per assorbimento,
si veda para. 5), hanno livelli più elevati di altri disposti nella fascia più alta dello spettro.
L'equalizzazione consiste in una riduzione del guadagno del preamplificatore, di 6 dB/ottava, con
il decrescere della frequenza; questa pendenza non compensa perfettamente quella del mare (-5 dB/ottava)
ma data la semplicità di realizzazione viene comunemente adottata.
L'amplificatore in oggetto esegue il taglio di 6 dB/ottava grazie ad un circuito RC realizzato come
mostra la figura 4, nella quale il condensatore C può essere la capacità stessa dell'idrofono idr.
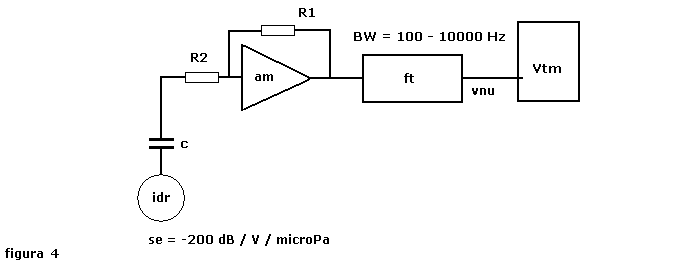
La funzione di trasferimento dell'amplificatore è:
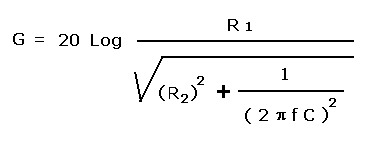
il cui andamento, in forma logaritmica, è visibile in figura 5; per f = 10000 Hz G = 86 dB:
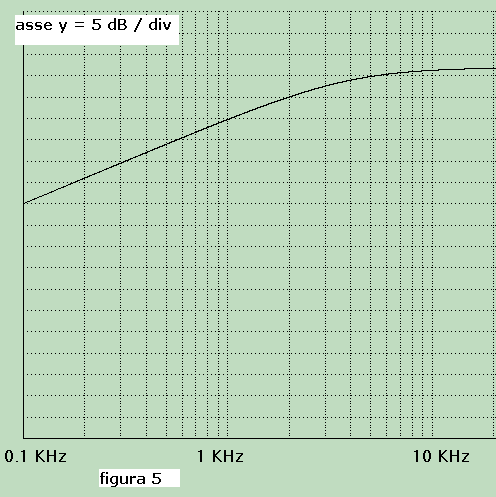
Data la nuova risposta dell'amplificatore si deve valutare lo spettro del mare, per ss = 2, modificato
dall'equalizzazione; il nuovo spettro, i cui livelli s'immaginano alterati dalla curva di figura 5, è
tracciato in figura 6:
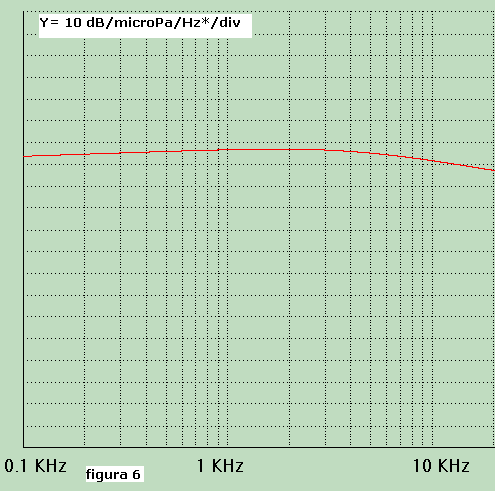
Si deve ricordare che questa nuova curva ha livelli già idealmente modificati da am secondo la
risposta di figura 5, pertanto nei calcoli a seguire non comparirà più il guadagno di am.
Per calcolare la v3nu con lo spettro indicato si deve rivalutare, per essa, il rumore del mare (SS = 2) come
segue:
- si valuta la frequenza centrale della banda secondo la media geometrica degli estremi:
f = ( 100 Hz x 10000 Hz)½ = 1000 Hz
- in figura 6 per f = 1000 Hz si ha : + 137 dB/microPa/Hz*
- il rumore complessivo in banda 100-10000 Hz è dato da:
PBW = + 137 dB/microPa/Hz* + 10 Log( 10000 Hz - 100 Hz) = 177 dB/microPa/BW
La v3nu all'uscita del filtro di figura 4 sarà:
v3nu = PBW + se - at = +177 dB/microPa/BW - 200 dB/volt/microPa - 6 dB =
= -29 dB/V = 35 mV eff.
A chiusura di questa pagina non resta che calcolare i livelli in uscita dal filtro di figura 4
delle due sorgenti acustiche, già simulate in paragrafo 5,):
Indicati con Ls1 e Ls2 i loro rispettivi livelli indice ripetiamo il computo:
-Ls1 = + 150 dB/microPa/BW1 a 300 Hz: BW1 = 200 Hz
-Ls2 = + 150 dB/microPa/BW2 a 9000 Hz: BW2 = 200 Hz
Ls1 e Ls2 subiranno un'attenuazione uguale per divergenza sferico-cilidrica di:
att = 60 dB + 10 Log 20 Km = 73 dB
Ls1 subirà un'attenuazione per assorbimento (vedi curva bianca figura2) pari a:
atas1 = 1 div x 0.01 dB/div x 20 Km = 0.2 dB ( si legga 0 dB)
Ls2 subirà un'attenuazione per assorbimento (vedi curva blu figura2) pari a:
atas2 = 9 div x 0.1 dB/div x 20 Km = 18 dB
Concludendo : Ls1 subirà un'attenuazione totale di 73 dB e Ls2 di 91 dB ; quindi
s1 colpirà il trasduttore con un livello di pressione :
Ps1 = 150 dB/microPa/BW1 - 73 dB = 77 dB/microPa/BW1
s2 colpirà il trasduttore con un livello di pressione :
Ps2 = 150 dB/microPa/BW1 - 92 dB = 58 dB/microPa/BW2
La tensione in uscita dal filtro di figura 4 sarà:
per s1:
vns1eq = Ps1 + se + g(a 300 Hz) - at = +77 dB/microPa/BW1 - 200 dB/v/microPa + 65 dB - 6 dB =
= - 63 dB / volt = 0.6 mv eff
per S2:
vns2eq = Ps2 + se + g(9000Hz) - at = +58 dB/microPa/BW2 - 200 dB/v/microPa + 85 dB - 6 dB =
= - 62 dB / volt = 0.7 mv eff
Da questi dati risultano i nuovi rapporti segnale/disturbo (r1'; r2') tra vns1eq, vns2eq e il rumore del
mare v3nu all'uscita del filtro:
r1' = vns1eq/v3nu = 0.6 mv eff / 35 mv eff : (s/n)dB = -35 dB
r2' = vns2eq/v3nu = 0.7 mv eff / 35 mv eff : (s/n)dB = - 34 dB
Confrontando i valori ora calcolati con gli analoghi computati senza equalizzazione abbiamo:
r1' = -35 dB
r1 = -25 dB
a 300 Hz l'equalizzazione provoca un peggioramento di s/n pari a 10 dB
r2' = -34 dB
r2 = - 44 dB
a 9000 Hz l'equalizzazione provoca un miglioramento di s/n pari a 10 dB
Il confronto dati ora mostrato è relativo ai casi specifici presi ad esempio; cambiando livelli
e frequenze di lavoro nuove indagini devono essere condotte secondo la stessa procedura.
Questa assunzione è stata fatta per non rendere più difficoltoso, di quanto già non sia, l'esame delle
diverse condizioni del rumore del mare. La presente appendice tratterà del rumore elettronico di am
per confrontarlo con le diverse condizioni operative.
Il rumore (ne) di un preamplificatore, generato dall'agitazione termica degli elettroni all'interno di gran
parte dei componenti che lo costituiscono, è un fattore determinante nel contesto di tutte le problematiche
annesse alla scoperta sonar.
I segnali idrofonici captati dai sensori devono essere amplificati da dispositivi che non ne alterino
il loro rapporto con il rumore del mare. Per fare ciò viene posto come rumore del mare di riferimento il
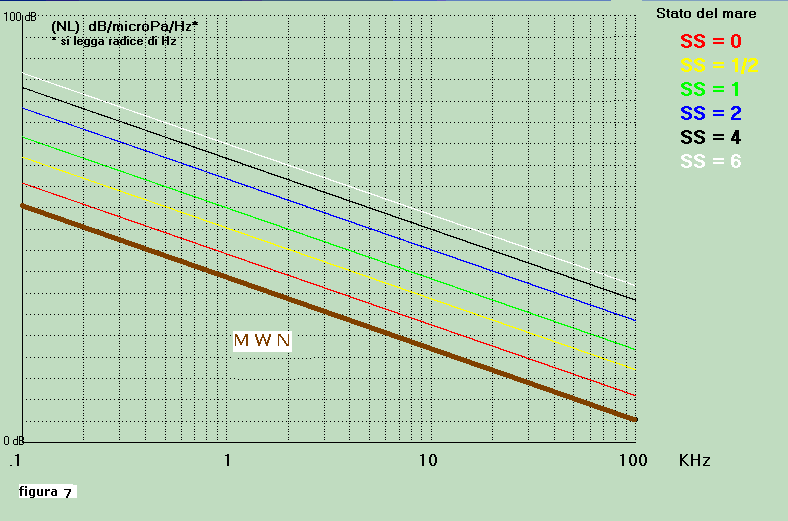
minimo fisicamente rilevabile; questo, dalle curve di Knudsen ampliate, è mostrate in figura 7.
La nuova curva (colore marrone) è indicata come "minimun water noise" (MWN), i suoi valori sono i minimi assoluti misurabili
in mare in condizioni estremamente particolari. Il livello del rumore elettronico (ne) dovrà
essere inferiore il più posiibile rispetto ai livelli delimitati dal MWN.
Il progetto accurato del preamplificatore è indirizzato ad ottenere, tramite la scelta meticolosa dei componenti,
i valori stabiliti di:
-guadagno
-risposta in frequenza
-risposta in fase
-dinamica
-rumore elettronico (ne)
Con accurati rilevi strumentali si verifica la rispondenza delle prime quattro caratteristiche richieste dal progetto.
Per il controllo di (ne), nella generalità dei casi, la procedura consiglia le misure all'uscita
dell'amplificatore in banda stretta (100 Hz) con adatto voltmetro selettivo; eseguite le stesse
entro la banda voluta i diversi valori sono riportati, idealmente, all'ingresso mediante la divisione
per il guadagno dell'amplificatore stesso e per la radice quadrata della banda secondo l'espressione:
Vni(f) = Vnu(f) - G (f) -10 Log DF
dove:
G (f): in dB (guadagno dell'amplificatore in funzione della frequenza)
Vnu(f): in dB/V/100 Hz (tensione di rumore all'uscita in banda 100 Hz)
Vni(f): in dB/V/Hz* (tensione di rumore riportata all'ingresso in banda 1Hz)
Df : banda d'analisi (100 Hz)
Per confrontare il rumore d'ingresso, calcolato in dB/volt/Hz*, con il rumore del MWN è necessario
trasformare detta curva in termini di tensione ipotizzando l'impiego di un idrofono,
di sensibilità nota, facente parte della base ricevente del sonar.
A titolo d'esempio possiamo utilizzare l'idrofono impiegato nelle misure di figura 3 e 4 che ha
una sensibilità di: -200 dB / volt /microPa.
Se esaminiamo ora la figura 7 osserviamo che le ordinate sono espresse in dB/microPa/Hz*, tra un minimo
di 0 dB ed un massimo di 100 dB; sommando a tali valori la sensibilità dell'idrofono di - 200 dB/V/microPa si ha un cambiamento
delle ordinate da -200 dB/V/Hz* minimo a -100 dB/V/Hz* massimo adatta al confronto proposto
così come indicato in figura 8 nella quale sono stati riportati, ad esempio, una serie di ipotetici
valori di Vni espressi in dB/V/Hz* ottenibili dalle misure e dai calcoli sopra indicati.
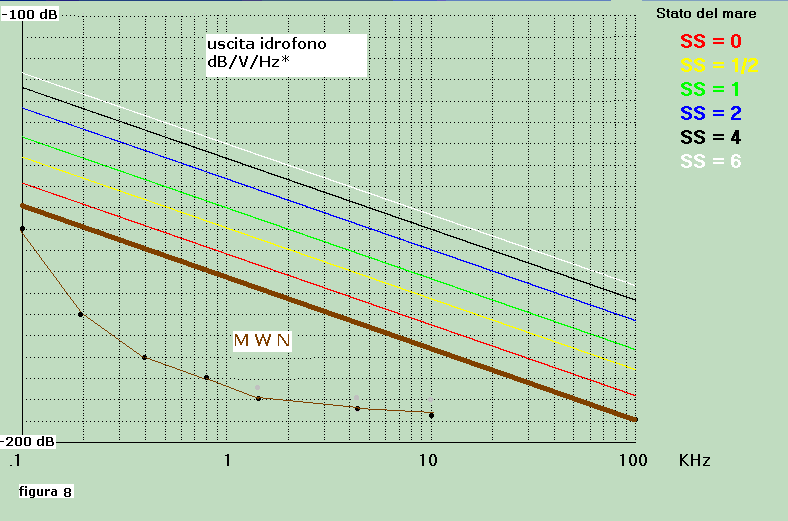
I valori di Vni(f) indicati ad esempio nella figura sono tutti inferiori al MWN, rispettivamente:
a 100 Hz : -5 dB
a 200 Hz : -20 dB
a 400 Hz : -25 dB
a 800 Hz : -25 dB
a 1600 Hz : -25 dB
a 3200 Hz : -20dB
a 10000 Hz : -15 dB
Questi risultati ipotetici sono discreti ma ancora lontani da un sistema ottimizzato; lavorando sul
progetto e sulla ricerca di semiconduttori a più basso rumore per i primi stadi dell'amplificatore
si possono ottenere risultati migliori.
Si fa presente che in casi estremamente particolari la riduzione di (ne) si ottiene inoltre tenendo
i preamplificatori idrofonici a temperature controllate molto basse.
Home