Sulla convergenza dei raggi acustici in mare

1)Premessa
Sulla convergenza dei raggi acustici in mare abbiamo accennato alla fine di pagina p252, in questa pagina cercheremo di ampliarne i concetti per arrivare alla formulazione di elementi utili a calcoli di massima sul fenomeno.
La convergenza dei raggi acustici si verifica quando il bativelocigramma presenta un profilo simile a quello mostrato in figura 1 nel quale la velocità del suono "V1" si riscontra sia in superficie, sia ad una profondità "hc" inferiore dalla profondità "H" del fondo:

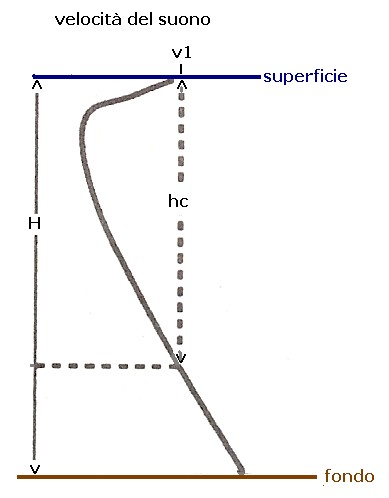figura 1:

2)L'attenuazione del suono in acque molto profonde
Prima d'iniziare l'esame del fenomeno della convergenza vediamo come, in acque molto profonde e bativelocigramma rettilineo, caso ideale di figura 2:

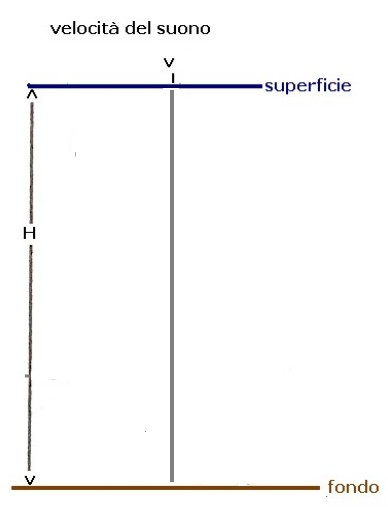figura 2:

si sviluppi la propagazione delle onde acustiche; questa può essere considerata di tipo sferico; rispondente perciò alla legge di attenuazione:
att(dB) = 20 Log (R)      1)
dove R è la distanza in metri.
in figura 3 è tracciata la funzione 1) per R variabile da 0 a 100000 m, in questo intervallo di distanza il suono viene attenuato per divergenza di 100 dB (in questo esempio non si tiene volutamente conto dell'aggiuntiva attenuazione per assorbimento):

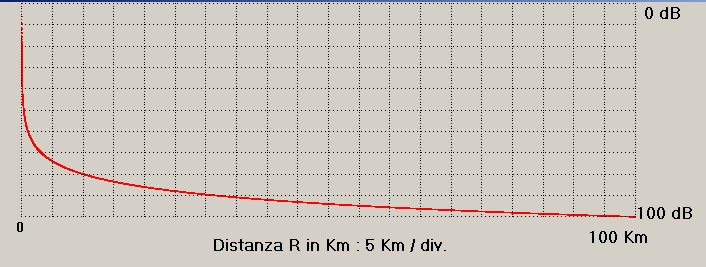figura 3

3) Come si presenta il fenomeno della convergenza
Quando il profilo del bativelocigramma è simile a quello mostrato in figura 1, nel quale la velocità di propagazione del suono è V1 sia in superficie che a quota "hc" dove hc < H, si generano una serie di percorsi dei raggi acustici che ondulano tra il punto d'emissione, considerato in questo esempio a circa -5 m, e il fondo, a circa 200 m, per convergere in diverse zone della superficie come mostra la figura 4:

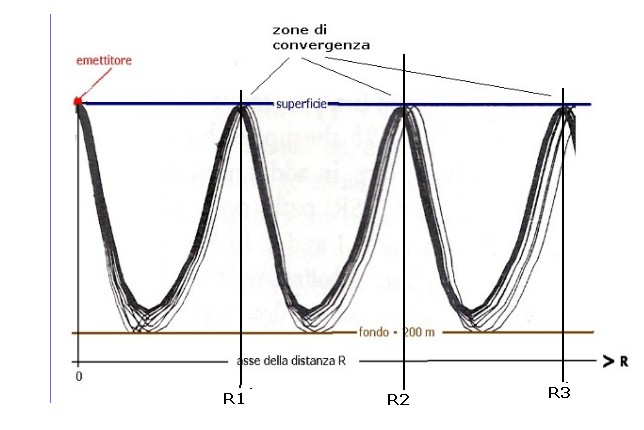figura 4

Come si intuisce dalla figura 4 le zone di convergenza, solo tre nel grafico alle distanza R1; R2; R3, sono molteplici e si distribuiscono nello spazio subacqueo consentendo l'ascolto dei segnali acustici a distanze molto elevate.

4) L'effetto generato dalle zone di convergenza
Nelle zone di superficie dove convergono i raggi riflessi dal fondo si ha una sorta di sommatoria tra i molteplici contributi energetici sì da incrementare il livello del segnale dai 10 ai 20 dB.
L'incremento in oggetto modifica la curva d'attenuazione di figura 3 tale che in corrispondenza delle distanze R1, R2... nelle quali si generano le zone di convergenza si ha un complessivo decremento dell'attenuazione così come mostra la figura 5 ricavata dalla 2 sommando alle distanze R1, R2...gli incrementi del livello che di fatto, in tali zone, riducono l'attenuazione per divergenza:

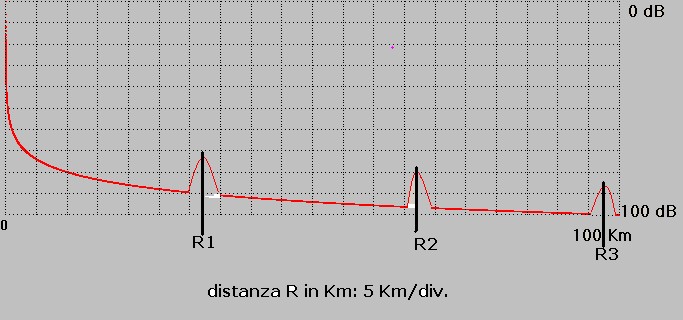figura 5

5) Su alcuni numeri legati al fenomeno della divergenza
Prendiamo ad esempio il caso ideale in cui due mezzi subacquei si trovino nella tipologia di attenuazione del suono indicata dalla figura 3 in uno scenario quale quello di figura 6:

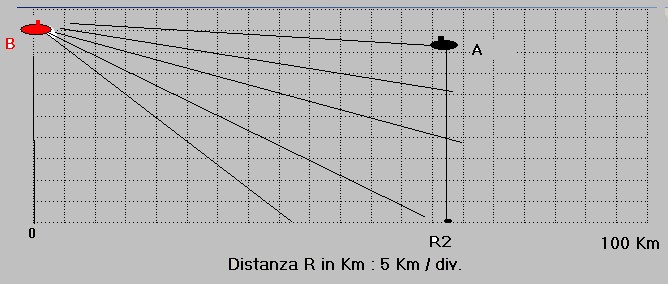figura 6

In figura 6 s'ipotizza il bersaglio "B" che emette rumore e il mezzo "A" che lo riceve con il sonar tramite onde acustiche che si propagano da "B" ad "A" secondo i raggi di una sfera.
La distanza tra i due mezzi, indicata con R2, è di circa 67 Km.
In queste condizioni ideali se "B" genera un livello di pressione acustica di 135/db/μPa/Hz
e le variabili al contorno del sonar "A" sono:

Banda d'ascolto = 1000-18000 Hz
NL = 55 dB/μPa/Hz
DI = 10 dB
RC = 2 Sec.
"d" = 1

alla distanza R2 = 67 Km il sonar di "A" , fissata la soglia di falso allarme: Pfa = 20 % , per "d = 1", potrà avere una probabilità di scoperta dell'ordine di : Priv = 55%.
Se i semoventi navali illustrati nel contesto dello scenario di figura 6, fossero collocati, alla stessa distanza R2 = 67 Km, ma coinvolti in una propagazione di convergenza si potrebbero rappresentare come in figura 7:

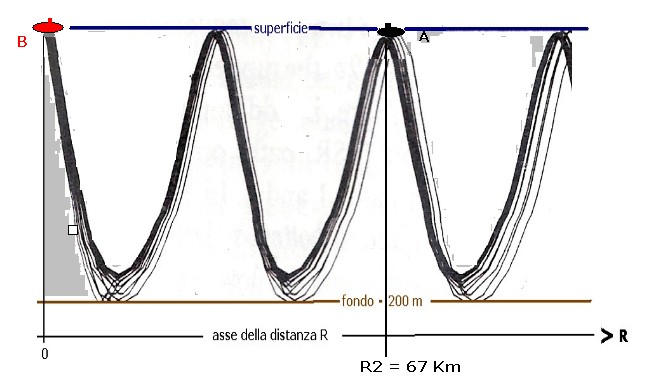figura 7

In queste nuove condizioni, grazie al decremento dell'attenuazione nelle zone di convergenza, assunto ad esempio in circa 10 dB, il sonar di "A" potrebbe scoprire il bersaglio "B" con una probabilità di scoperta Priv = 99 % e, pur alzando la soglia a livelli dell'ordine di Pfa = 0.1 % ; prestazioni eccezionali per distanze così elevate.

6) Sulle modalità di calcolo dei dati del paragrafo 5)
Per lo sviluppo dei calcoli precedenti si dovrebbe intervenire con processi analitici molto complicati; grazie però all'impiego in modalità iterativa sia del calcolatore delle curve ROC di pagina p80 che del calcolatore SONARMATH di pagina p6 i risultati, a carattere indicativo, si ottengono in un ragionevole lasso di tempo.
Tutto il calcolo si articola, una volta posto R2 costante ( R2 = 67 Km ) come risultato della computazione dell'equazione della portata di un sonar passivo che abbia in un primo caso (propagazione di tipo sferico di figura 6) le variabili elencate nel paragrafo 5) con "d" = 1 ; per Priv = 55 % e Pfa = 20 % : ed in un secondo caso ( propagazione in zona di convergenza di figura 7) un valore del parametro "d" ( d = 28 ; per Priv = 99% e Pfa = 0.1 % ) adatto a compensare il decremento di 10 dB dell'attenuazione alla distanza R2

Home

Stampa immagine grafica o descrizione testuale