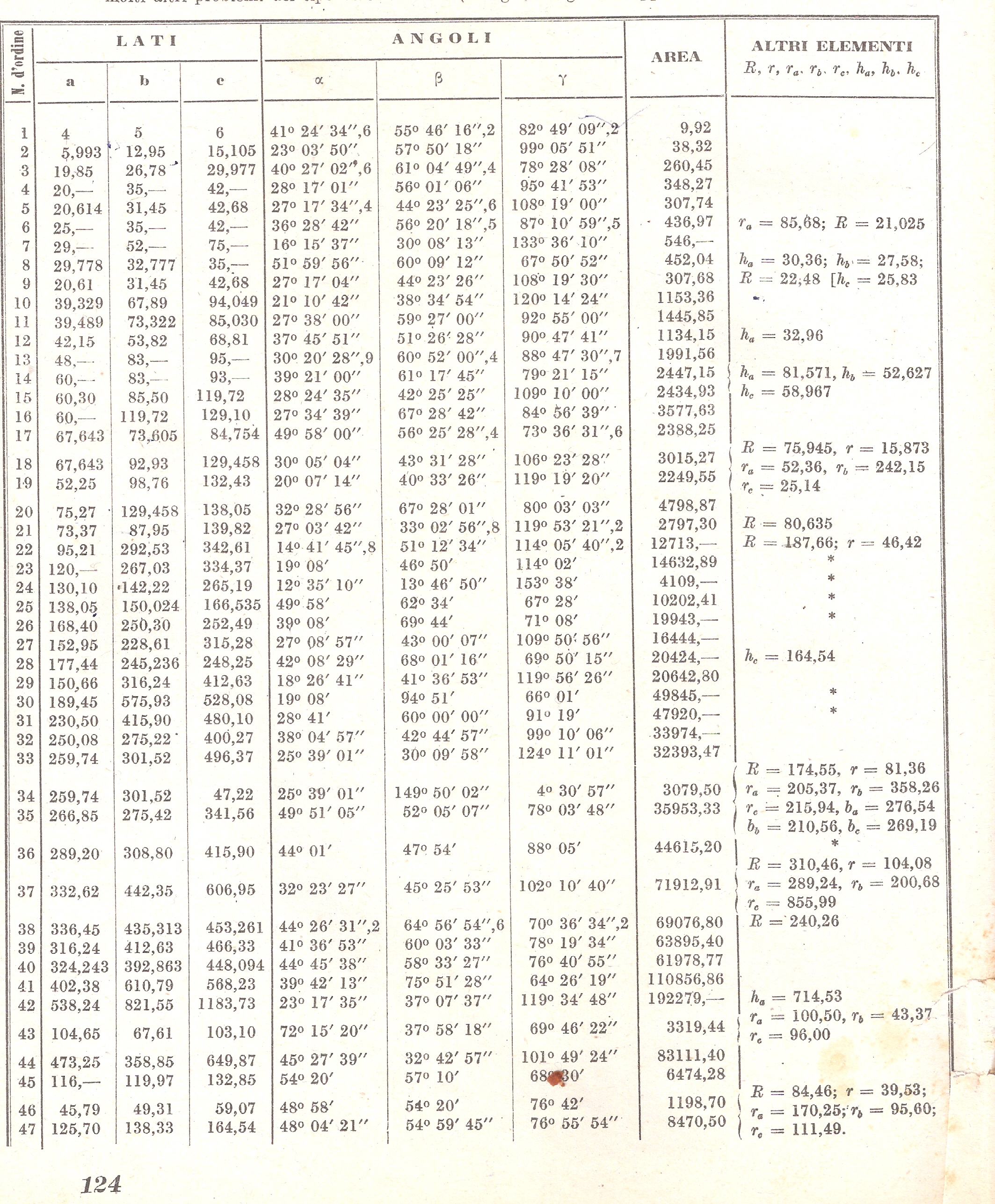
SONAR-INFO-203
Triangoli qualunque
-soluzioni secondo il teorema dei seni: precisione ad 1'' -
noti un lato e due angoli adiacenti
1)Un triangolo qualunque e i suoi elementi
In figua 1 Ŕ tracciatio un triangolo qualunque con tutti i suoi elementi, distinti da lettere ed angoli, ai quali faremo riferimento nel prosieguo del lavoro.
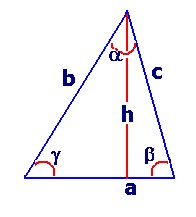 figura 1
figura 12)Lo strumento di calcolo
Per la soluzione dei triangoli qualunque, in particolare avendo come elementi noti un lato e due angoli adiacenti, Ŕ stato sviluppato un file eseguibile con il quale, in base alla prescelta terna di elementi si computano rapidamente tutti gli altri con una precisione di 1'' ( un secondo in gradi sessagesimali ).
Il pannello operativo del calcolatore Ŕ mostrato in figura 2:
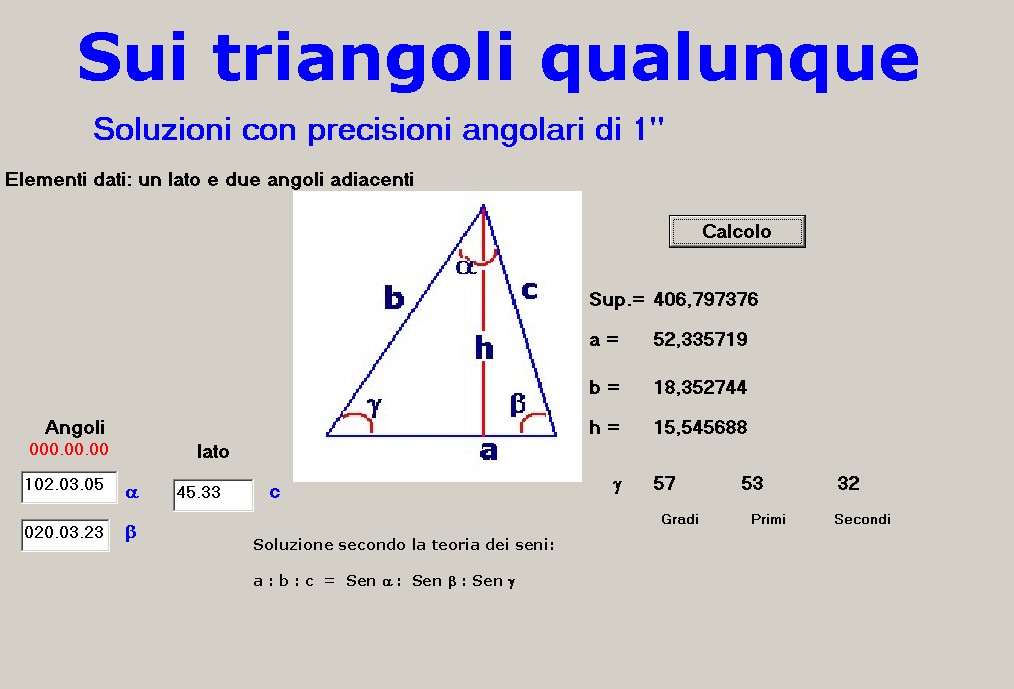 figura 2
figura 2L'impiego del calcolatore Ŕ semplice; facendo riferimento alla figura 2 vediamo il caso in cui la terna di elementi noti sia:
alfa = 102░ 03' 05''
beta = 020░ 03' 23''
c = 45.23
Gli elementi del triangolo, calcolati secondo il teorema dei seni, sono mostrati a destra dopo la pressione del pulsante "Calcolo"
3)Attenzione nell'inserimento dei dati angolari
Dovendo inserire valori angolari espressi in gradi sessagesimali, come ad esempio nel caso precedente ( gradi; primi; secondi ) si deve seguire la particolare procedura:
La fase d'inserzione lell'angolo deve avvenire nella sequenza:
si digita il numero dei gradi 102
si digita un punto di separazione .
si digita il numero dei primi 03 si digita un punto di separazione .
si digita il numero dei secondi 05
in modo che la scritta nella finestra appaia come sotto:
102.03.05
Se il numero dei gradi occupa soltanto due cifre, supponiamo;
75░ 37' 4''
si deve digitare:
075.37.04
4)Esercitazioni
Per sviluppare esercitazioni sul calcolatore cliccare sull'eseguibile Poligonali-1, quindi, in base alla tabella sotto riportata, scegliendo a piacere coppie di dati, si possono fare numerosi esercizi per avere riscontri sull'impiego del calcolatore