SONAR-INFO-p199
L'integrale di Sievert
(3░ della serie degli integrali particolari)
-Calcolo automatico del valore numerico tra i limiti d'integrazione per gli integrali definiti-
1) GeneralitÓ
Con questa pagina si apre la 3^ di una serie di routine per il calcolo degli integrali definiti a carattere particolare: l'integrale di Sievert.
La funzione integranda, e quindi l'integrale, sono funzioni parametriche in "X"
Le tabelle dell'integrale, calcolato in funzione del limite d'integrazione superiore "Θ" per gli angoli da 10░ a 90░ a passi di 10░ e del parametro "X" da 0 a 10, in sette intervalli, sono disponibili in letteratura per un numero finito di combinazioni tra "Θ" e "X"; con questa pagina proponiamo uno strumento di calcolo per infinite combinazioni di valori, sia nell'ambito degli estremi di tabella che al di fuori di essa.
2) L'integrale di Sievert
La forma analitica dell'integrale in oggetto, integrale di una funzione parametrica in "X", Ŕ sotto riportata:
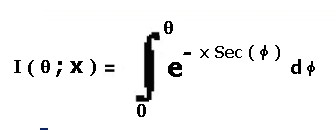
dove l'estremo superiore d'integrazione, "Θ" , si estende da 0 a 90░ e il parametro "X" da 0 a 10 ; entrambi i valori sono impostati dall'utilizzatore: nell'apposito Text Box per " X " in alto a sinistra, e secondo Text Box, subito sotto, per Θ, come mostra il pannello operativo di figura 1:
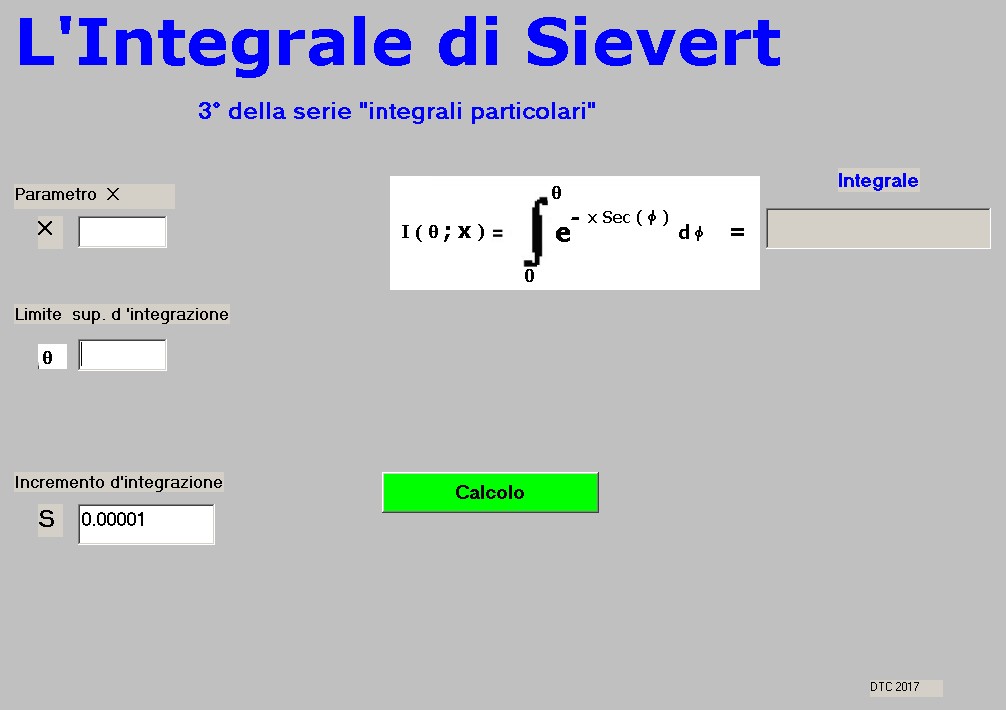 figura 1
figura 1Come si vede in figura un terzo Text Box, S, sotto il secondo, consente di stabilire l'incremento del processo d'integrazione fissato; il valore S sostituisce l'infinitesimo "dt" nel processo di calcolo di I( Θ; X ).
Al lancio del programma "S" Ŕ fissato a: S = 0.00001; questo Ŕ un incremento che consente senza alcun dubbio calcoli veloci con precisioni fino a sei decimali.
Il pulsante "Calcolo" a riposo Ŕ di colore verde, una volta premuto permane di colore rosso per tutto il tempo di calcolo; Ŕ un modo per giustificare il tempo d'attesa per lo sviluppo del processo.
3) Esempi di calcolo
Il calcolo dell'integrale si esegue chiamando l'eseguibile in VB6: IP3.exe che presenta la schermata di figura 1 .
I risultati degli esempi si confrontano con un dato tabellare preciso a 6 decimali:
a caso un valore calcolato per Θ = 20░ ed X = 2.6 il valore dell'integrale Ú: I(Θ; X) = 0.024582
-primo esempio:
Per S impostato in automatico al lancio del programma: S = 0.00001
e per X = 2.6 ed Θ = 20░, dopo un sensibile tempo di calcolo, si ha: I(Θ; X) = 0.024582 coincidente con il valore di tabella.
-secondo esempio:
Supponiamo che per velocizzare il calcolo s'imposti manualmente S: S = 0.01; per X = 2.6 ed Θ = 20░, si ha immediatamente : I(Θ; X) = 0.024583 con errore di circa 4 / 100000 rispetto al calcolo precedente.
-terzo esempio:
Un calcolo che mostra la versatilitÓ di questo sistema di computazione si pu˛ sviluppare per un valore di X; non compreso in tabella:
Pe X = 2.15 ed Θ = 30░ il valore di I(Θ; X) deve essere compreso tra I( 30░; 2 ) = 0.064492 e I( 30░; 2.2 ) = 0.0552329 di tabella :
il calcolo mostra l'asserto: I( 30░; 2.15 ) = 0.055136
-quarto esempio:
Sempre a dimostrare le caratteristiche del calcolatore possiamo computare un valore I(Θ; X) con Θ = 27░ e X = 3.6 non compresi in tabella: per dette variabili, per S = 0.00001, si ha:
I( 27░ ; 3.6 ) = 0.011272.