SONAR-INFO-p170
Correlazione con segnali limitati
Il calcolo rapido di tutte le variabli
1) GeneralitÓ 2)Sulle variabili e gli algoritmi di correlazione 3)Il file.exe per il calcolo rapido delle variabili 4)Esempio d'impiego di Rpdcr
In questa pagina sono riassunti tutti gli algoritmi di calcolo relativi ai correlatori con
segnali limitati ampiamente trattati in p5; la ragione della sintesi risiede nell'esigenza
di ottenere rapidamente, mediante apposito file.exe, tutte le variabili del processo
di correlazione e la relazione finale che subordina
le probabilitÓ di rivelazione (Priv) e di falso allarme (Pfa) al rapporto segnale/disturbo
esistente nella coppia di segnali che, dall'uscita del filtro di banda, raggiungono i
circuiti di limitazione d'ampiezza del correlazione digitale.
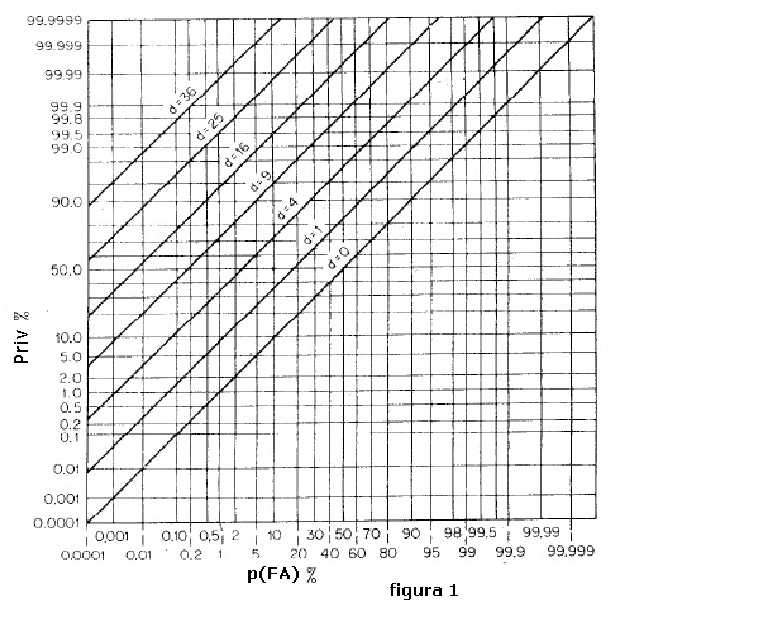
La determinazione della coppia Priv e Pfa si ottiene dal grafico di figura 1 in par.2
avvalendosi del valore del parametro d calcolabile secondo l'algoritmo riportato
al punto 16) di citato paragrafo.
Di seguito le numerose variabili e gli algoritmi relativi alla correlazione con segnali
limitati che, mediante opportuni passaggi e sostituzioni, danno vita al file.exe giÓ menzionato
in precedenza:
1)Simbolo della larghezza di banda dei filtri di precorrelazione: BW in Hz
2) Simbolo della costante di tempo dell'integratore: RC in Sec.
3)Simbolo del livello di segnale all'uscita dei filtri di banda applicato ai limitatori
del correlatore: Si
4) Simbolo del livello di rumore all'uscita dei filtri di banda applicato ai limitatori
del correlatore: Ni
5) Simbolo del rapporto tra Si ed Ni in termini lineari: SNi
6) Simbolo del rapporto tra Si ed Ni in termini logaritmici: SNidb = 20 Log SNi
7) Simbolo dell'ampiezza normalizzata del segnale all'uscita del correlatore: Su
8) Algoritmo, in termini lineari, per il calcolo di Su:
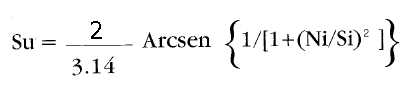
9) Simbolo dell'ampiezza normalizzata del rumore (varianza) all'uscita del correlatore: Nu
10) Algoritmo, in termini lineari, dell'ampiezza normalizzata del rumore Nu all'uscita del correlatore:
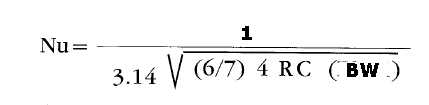
11) Simbolo del rapporto segnale/ rumore all'uscita del correlatore:
- in termini lineari: Su / Nu
- in termini logaritmici: SNudb = 20 Log ( Su / Nu )
12) Algoritmo del rapporto Su/Nu in termini lineari
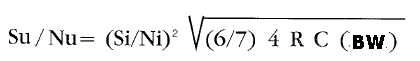
13) Simbolo del parametro delle curve ROC : d, da esso dipendono le coppie (Priv; Pfa):
14 )Algoritmo, in termini lineari, del parametro d ;
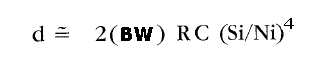
15) Simbolo del guadagno di processo Gpr in termini logaritmici:
Gpr = SNudb - SNidb
16) In figura 1 le curve ROC dalle quali estrapolare, in base al valore del parametro d, le
infinite coppie di combinazioni (Priv; Pfa) :
Il file al titolo, nominato Rpdcr.exe, una volta avviato si presenta con la schermata
visualizzata in figura 2:
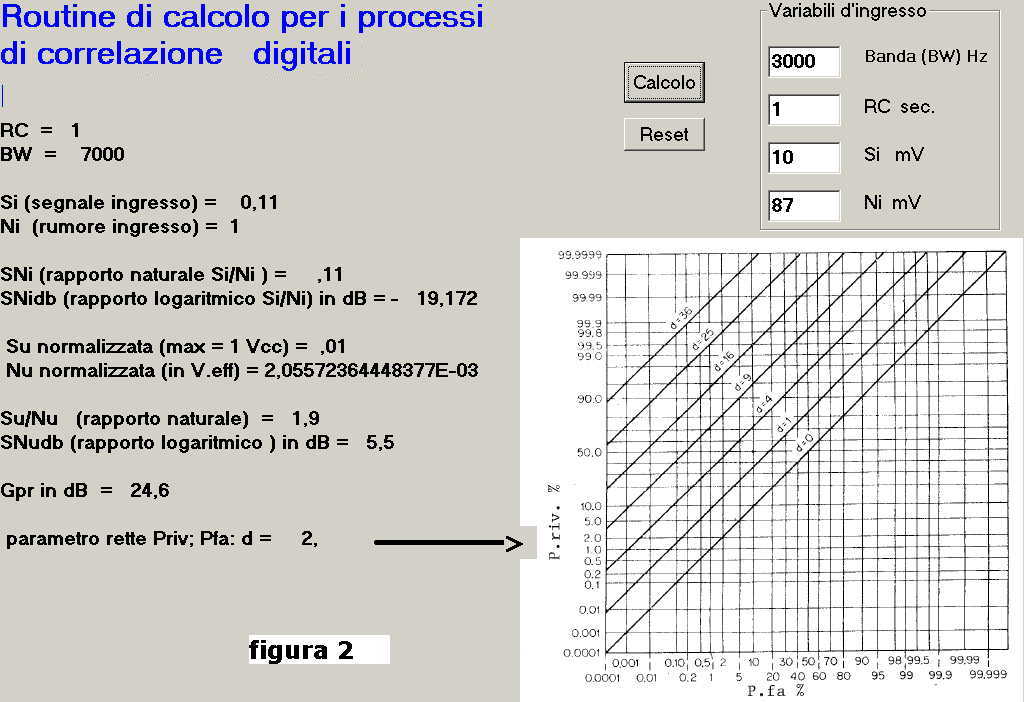
Nella schermata sono presenti, a destra in alto, quattro caselle d'inserzioni dati quali:
-La banda di lavoro BW in Hz
-La costante d'integrazione RC in Sec.
-Il livello del segnale d'ingresso al correlatore Si in mV eff
-Il livello del rumore d'ingresso al correlatore Ni in mV eff
Con il pulsante "Calcolo" si procede all'attivazione della routine di calcolo e
alla presentazione dati; si ripete il processo cancellando i dati passati
con il pulsante "Reset".
I dati calcolati, che caratterizzano completamente il processo di correlazione, sono
presentati a sinistra dello schermo come segue:
SNi ; SNidb ; Su ; Nu ; Su/Nu ; SNudb ; Gpr in dB , parametro "d"; con quest'ultimo e con
il diagramma delle curve ROC si determina una coppia di Priv e Pfa.
Si debba risolvere il seguente problema:
Dati i livelli di segnale e di rumore in banda BW = 7000 Hz, rispettivamente di:
Si = 0.112 mV eff.
Ni = 0.86 mv eff.
e disponendo una costante di tempo RC = 1 Sec.
determinare tutte le variabili che caratterizzano il correlatore e una coppia di valori
Priv e Pfa, a piacere, congrua con l'insieme delle variabili calcolate.
Dopo l'inserzione delle 4 variabili d'ingresso BW:RC;Si;Ni e pigiando il pulsante "Calcolo"
si ha la seguente schermata dati di figura 3:
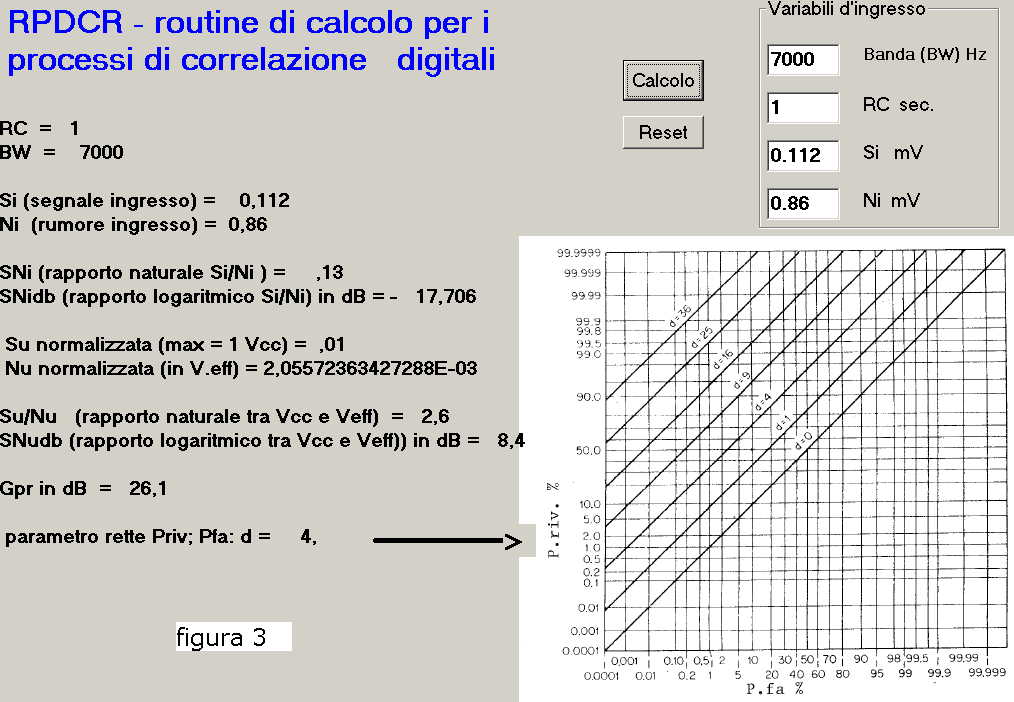
I dati presentati sono stati calcolati secondo gli algoritmi riportati nel paragrafo 2) e
definiscono tutte le variabili coinvolte nel processo di correlazione a segnali limitati;
inoltre con il valore del parametro d = 4 Ŕ ora possibile determinare una qualsiasi
coppia di (Priv; Pfa) individuabile nel grafico curve ROC sulla retta d = 4.
In base alle esigenze operative si possono scegliere coppie diverse di (Priv; Pfa) in base
alla voluta impostazione della soglia di rivelazione ( si veda p108 ed altre ) ;
ad esempio se si desidera un elevato valore di Priv, supponiamo il 70%, dovremo accettare
una probabilitÓ di falso allarme pari a: Pfa = 10% infatti questa coppia di valori Ŕ individuata
dalla retta con parametro d = 4.
Diversamente se si vuole ridurre la probabilitÓ di falso allarme a: Pfa = 0.01 % si dovrÓ
accettare una modesta probabilitÓ di scoperta con un valore di Priv ≈ 30 % .
Qualsiasi coppia (Priv; Pfa) individuata dalla retta d = 4 pu˛ essere scelta sulla base del
criterio di soglia adottato.