SONAR-INFO-p126
Le funzioni integrali
Calcolo del valore numerico tra i limiti d'integrazione
Il calcolo del valore numerico delle funzioni integrali non sempre si presta ad essere affrontato in modo semplice; in alcuni testi di matematica applicata sono disponibili numerose tabelle con le quali è possibile ricavare il valore degli integrali definiti in particolari campi di variabilità degli estremi d'integrazione.
Nelle computazioni relative alle tematiche sonar, riportate nel presente sito, sono state utilizzate, sia le tabelle, sia particolari algoritmi di calcolo appositamente studiati per le necessità contingenti; nell'intento di far cosa utile al lettore di questa pagina sono proposte, tramite un particolare file.exe ( INTEGRALMATH ) le più ricorrenti funzioni integrali che consentono il calcolo rapido del valore numerico dell'integrale definito prescelto dall'operatore.
Nelle tabelle citate i valori numerici sono definiti con un numero di cifre generalmente molto elevato, da 4 a 10, nella routine di INTEGRALMATH la precisione è limitata a 5 decimali.
Nei calcoli automatici, essendo I = ∫ f(t) dt, ovvero la sommatoria dei prodotti [ f(t) dt ], la precisione dipende dall'ampiezza dall'incremento dt di elaborazione selezionato dall'operatore ; riducendo l'infinitesimo dt si aumenta la precisione ma anche il tempo di macchina necessario al calcolo.
Sarà l'operatore sulla base delle proprie necessità di calcolo a stabilire un ragionevole compromesso.
2) Le funzioni integrali disponibili
La raccolta delle funzioni integrali disponibili nel file eseguibile è esposta qui di seguito senza alcun ordine, ne di complessità, ne di importanza, indicandone il nome ed esplicitandone la formula:
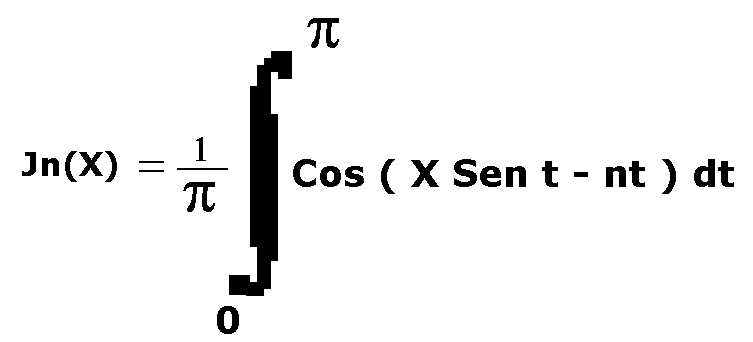
1) funzioni di Bessel: ordine n = 0;1;2; ...
2) funzione d'errore
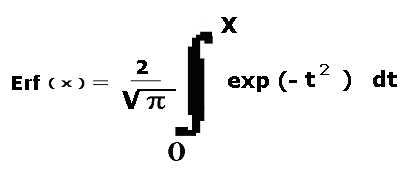
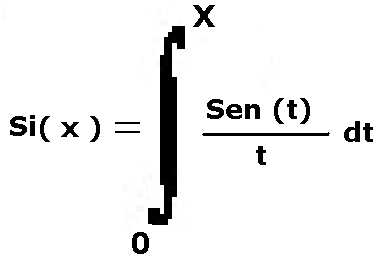
3) integralseno
4) integralcoseno
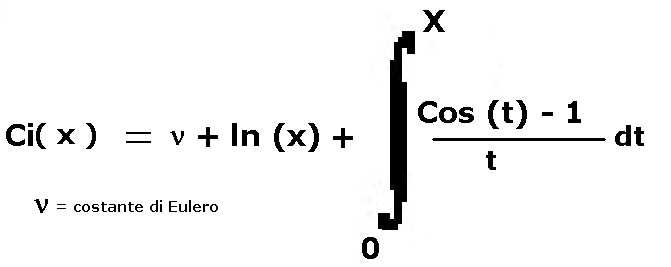
Il valore di ν che compare nella formula (costante di Eulero) vale ν = 0.5772156649..
5) esponenziale integrale
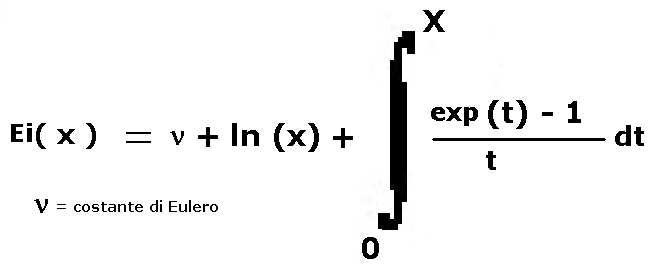
Il valore di ν che compare nella formula (costante di Eulero) vale ν = 0.5772156649..
6) funzione gamma
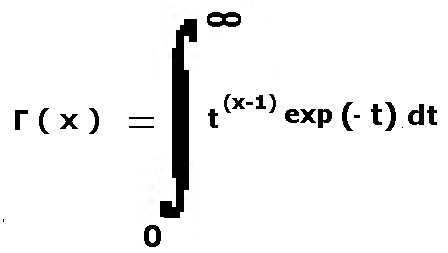
Nella funzione Gamma il limite superiore d'integrazione è infinito, per la computazione tecnica si consente all'operatore d'inserire il valore più elevato possibile di tale limite, compatibilmente dal tempo richiesto dal computer per eseguire l'operazione.
7) integrale di Dawson
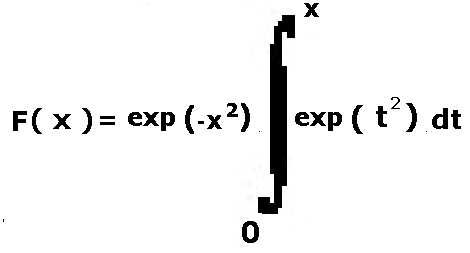
8) integrale di Fresnel
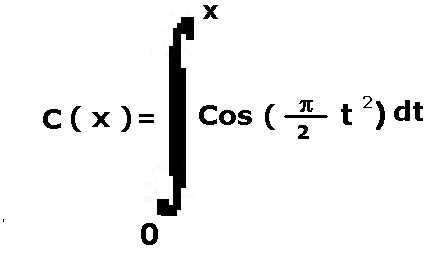
Per ciascuna delle 8 funzioni integrali è disponibile, tramite la pagina di selezione di "INTEGRALMATH" mostrata in figura 1, la sezione applicativa con la schermata di lavoro:

Per assicurare sempre una buona precisione di calcolo si consiglia di porre il valore del dt il più piccolo possibile, sempre chè la velocità della macchina consenta una elaborazione in tempi ragionevoli.
3)L'applicativo per le funzioni di Bessel
Una volta selezionate, tramite l'apposito pulsante in figura 1, le funzione di Bessel se ne devono stabilire le variabili richieste dalla routine:
nelle apposite finestre di figura 2 si:
-seleziona l'ordine della funzione di Bessel desiderato; 0, 1, 2 ( scelta d'esempio n = 1 )
-s'imposta la variabile x ( scelta d'esempio xo = 0.4513 )
-s'imposta il valore del dt di calcolo ( ad esempio dt = 0.00001 )
Una volta terminata l'immissione dati si pigia il pulsante "Calcolo" e si attende che compaia il valore dell'integrale definito J1(xo); sotto il pulsante si sviluppa un segmento rosso che indica come la routine di calcolo sia in azione, la comparsa di un cerchietto all'estremo destro indica che il calcolo è ultimato:
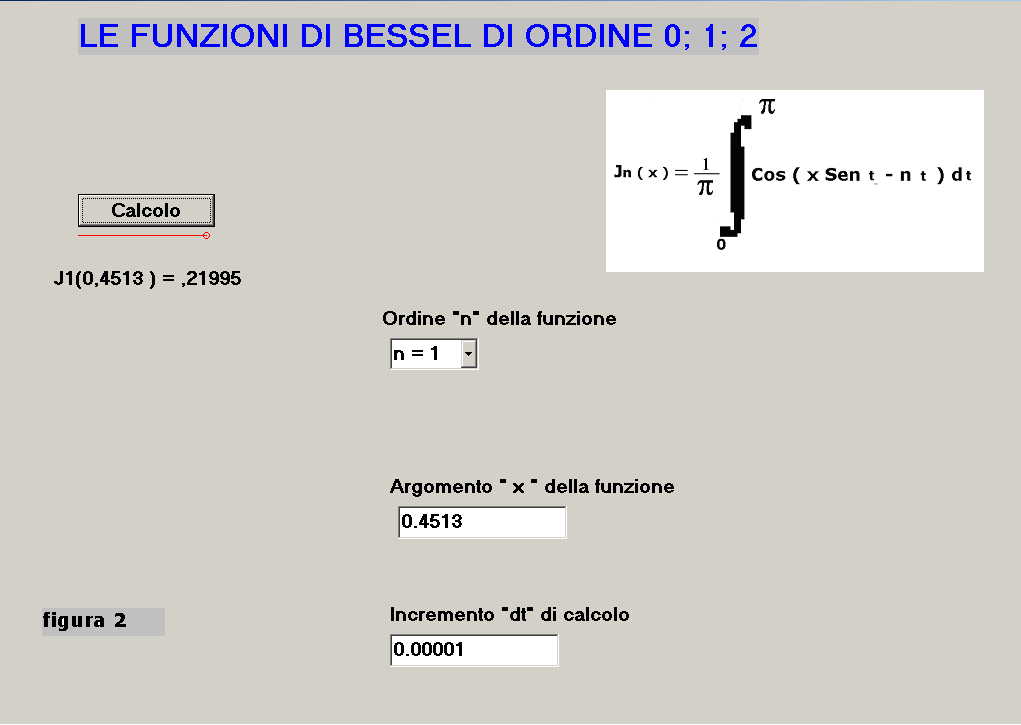
Come si vede il valore calcolato di J1(0.4513) è J1(0.4513) = 0.21995; un valore così accurato non sarebbe stato deducibile secondo le tabelle dato che queste, generalmente definite a passi della variabile xo da 0.1, avrebbero potuto fornire soltanto i valori di J1(0.4) = 0.19602 per difetto o J1(0.5) = 24226 per eccesso.
Si osservi che la casella per l'immissione del dt è impostata al valore base di dt = 0.00001, tale valore può essere sostituito quando e come si voglia con altri valori d'incremento.
4)L'applicativo per la funzione d'errore
Una volta selezionata, tramite l'apposito pulsante in figura 1, la funzione d'errore se ne devono stabilire le variabili richieste dalla routine:
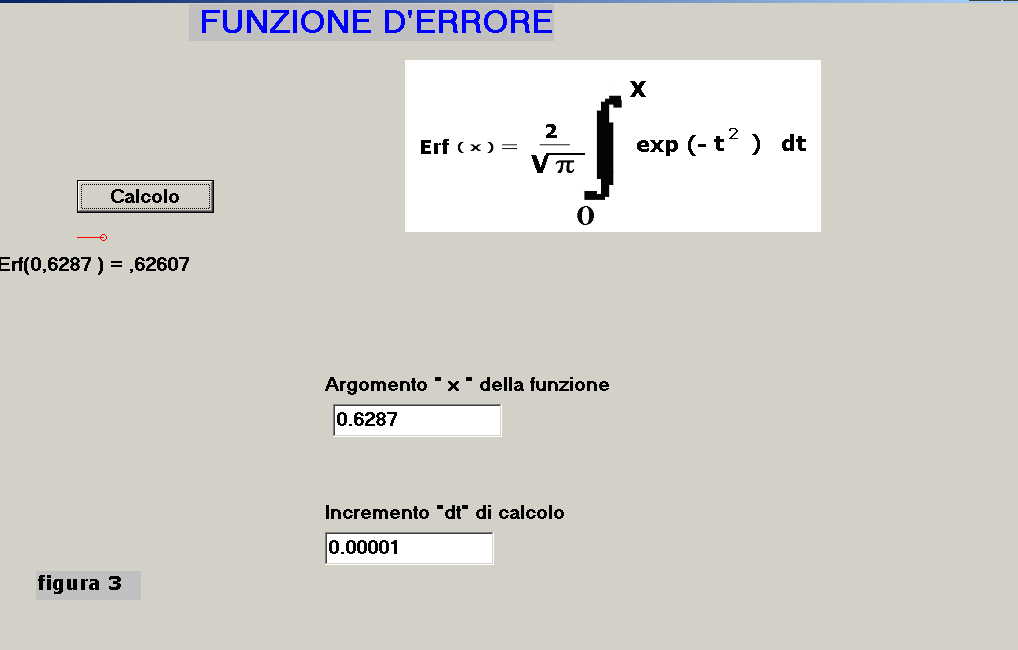
nelle apposite finestre di figura 3 :
-s'imposta la variabile x ( scelta d'esempio xo = 0.6287 )
-s'imposta il valore del dt di calcolo ( ad esempio dt = 0.00001 )
Una volta terminata l'immissione dati si pigia il pulsante "Calcolo" e si attende che compaia il valore dell'integrale definito erf(xo) ; sotto il pulsante si sviluppa un segmento rosso che indica come la routine di calcolo sia in azione, la comparsa di un cerchietto all'estremo destro indica che il calcolo è ultimato.
Dalla figura 3 si evince che per xo = 0.6287 il valore della funzione d'errore è: erf(0.6287) = 0.62607.
5)L'applicativo per la funzione integralseno
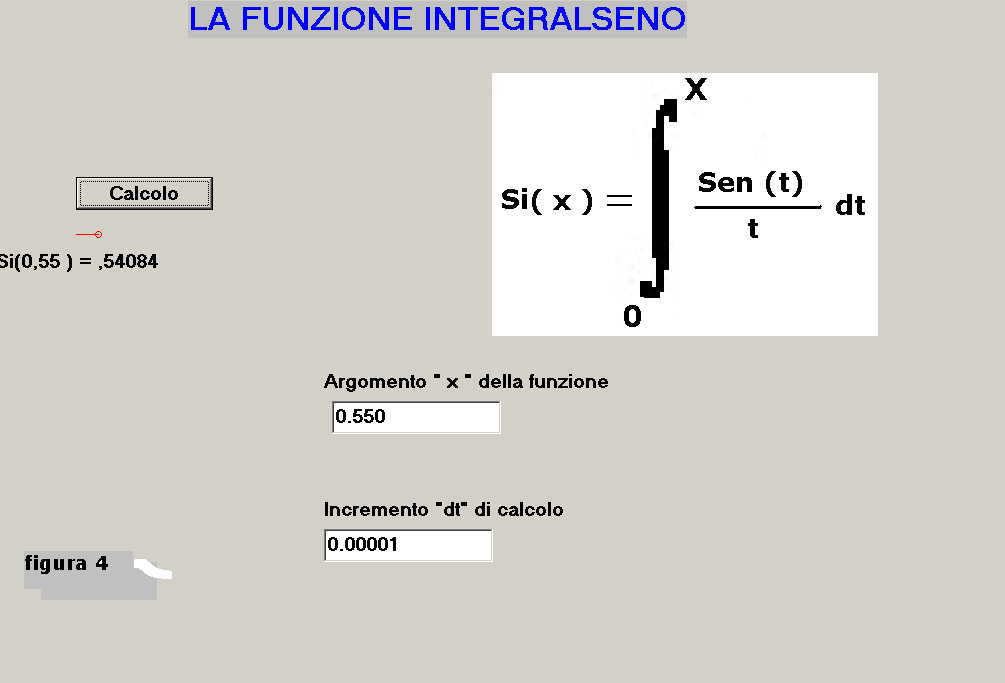
La procedura per l'immissione dati è come la precedente di paragrafo 4):
-s'imposta la variabile x ( scelta d'esempio xo = 0.550 )
-s'imposta il valore del dt di calcolo ( ad esempio dt = 0.00001 )
a seguito dell'azione sul bottone calcolo si ha la schermata di figura 4 con il risultato:
Si( 0.550 ) = 0.54084.
6)L'applicativo per la funzione integralcoseno
La procedura per l'immissione dati è la solita:
-s'imposta la variabile x ( scelta d'esempio xo = 0.3214 )
-s'imposta il valore del dt di calcolo ( ad esempio dt = 0.00001 )
a seguito dell'azione sul bottone calcolo si ha la schermata di figura 5 che indica il risultato:
Ci( 0.3214 ) = - 0.58357.

7)L'applicativo per la funzione gamma
Per il calcolo della funzione Gamma il limite superiore d'integrazione deve essere posto, tramite l'apposita finestra, ad un valore 10 o multiplo di 10; più elevato è il limite migliore è la precisione di calcolo; quindi posto ad esempio: ls = 10; xo = 1.135; dt = 0.00001 si ha:
Γ (1.135) = 0.93809 come mostrato in figura 6:

8)L'applicativo per la funzione esponenziale integrale
Dati: xo = 0.74 ; dt = 0.00001 con ν = 0.5772156649..
si ha il risultato mostrato in figura 7:

9)L'applicativo per la funzione di Dawson
Dati: xo = 0.7833 ; dt = 0.00001
si ha il risultato mostrato in figura 8:

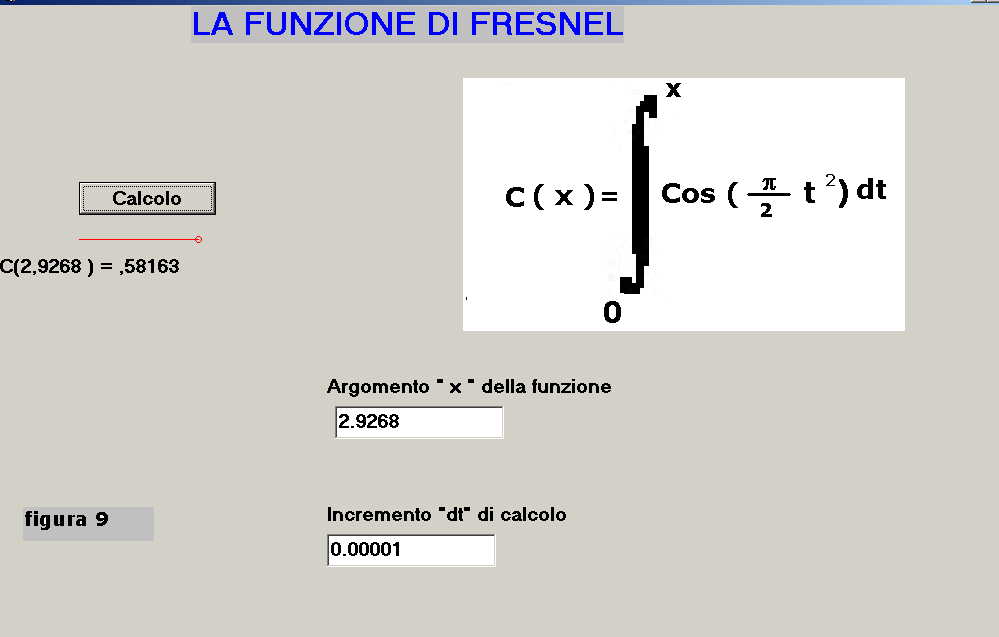
10)L'applicativo per la funzione di Fresnel
Dati: xo = 2.9268 ; dt = 0.00001
si ha il risultato mostrato in figura 9: