SONAR-INFO-p112

IL DIFFERENZIALE DI RICONOSCIMENTO E LA SOGLIA -3-
Sulla variabile Si/Ni della terna Si/Ni; P(FA); P(D)

1)Riepilogo delle formule per la correlazione a coincidenza di polarità
Lo sviluppo della presente pagina allo scopo di mostrare, da un punto di vista grafico-matematico, la relazione esistente tra le diverse grandezze che sono coinvolte nella determinazione della terna Si/Ni; P(FA); P(D) sulla quale abbiamo dissertato in p108 e p110; per far questo è necessario rivedere alcuni dettagli in merito ai metodi di correlazione impiegati per la rivelazione dei bersagli:
I metodi di cui abbiamo accennato sono basati sul trattamento di segnali limitati (segnali a due stati) con i quali si realizza la correlazione a coincidenza di polarità.
Questa tecnica, ampiamente descritta in p5 par 2.3, mostra le formule caratteristiche per il calcolo, sia del livello di segnale Crt, sia del disturbo Nux, all'uscita del correlatore.
La prima formula, di seguito riportata, indica come varia il livello del segnale Crt all'uscita del correlatore in funzione del rapporto Si/Ni d'ingresso



La funzione indicata è generalmente tracciata in coordinate cartesiane doppio lineari per mostrarne l'andamento in funzione di Si/Ni variabile in un intervallo compreso tra -60 dB e + 60 dB.
Nella figura 1 è riportata la funzione menzionata in forma normalizzata:



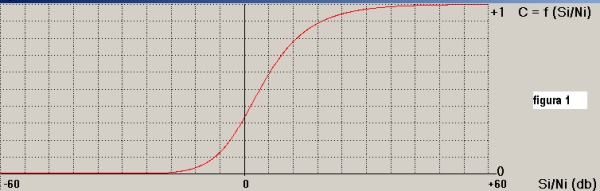
La curva che esprime Crt, in funzione del rapporto Si/Ni, evidenzia come l'ampiezza del segnale all'uscita del correlatore sia penalizzata dal decrescere di detto rapporto; questo fatto, in presenza della varianza Nux, influenza naturalmente la probabilità P(D) di rivelazione del segnale facente parte della terna Si/Ni; P(FA); P(D) di cui alle pagine p108 e p110.
La formula normalizzata che consente il calcolo del livello del disturbo Nux, espresso in valore di picco, all'uscita di un correlatore a coincidenza di polarità è sotto indicata:



Dove:
RC = costante di tempo di post integrazione (espressa in secondi)
(F2-F1) = banda dei segnali all'ingresso del correlatore (in Hz).

Come si nota dalla funzione Nux questa non dipende dal rapporto Si/Ni ma, essendo la conseguenza del particolare tipo di correlazione, dipende dal rapporto tra la banda dei segnali d'ingresso (F2-F1) e la banda Ft caratterizzata dalla costante di tempo RC.
Infatti, essendo Ft = 1 /(6.28 RC), il prodotto RC (F2-F1), indicato nella formula, può essere scritto RC (F2-F1) = (F2-F1)/6.28 Ft.

L'andamento della funzione Nux in dipendenza di RC è riportato in figura 2 per cinque diversi valori della banda d'ingresso:



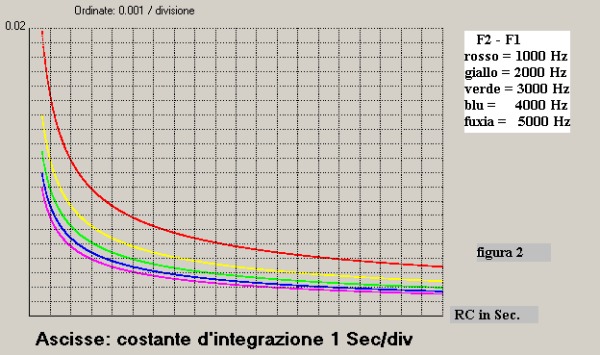
Confrontando ora la figura 1 con la 2 si vede che, date le notevoli differenze di scala, non è fattibile la comparazione grafica dei valori delle due curve per vedere come si posiziona il livello del disturbo Nux rispetto al livello del segnale Crt nei diversi casi pratici.
Il paragrafo seguente affronta e risolve questo problema.

2)L'ampliamento della scala per la funzione Crt
L'ampliamento della scala delle ordinate della figura 1 si realizza tracciando la curva Crt= f(Si/Ni) in un reticolo con ascisse lineari, estese da -28 dB a + 28 dB, e ordinate logaritmiche a tre decadi estese tra 0.001 a 1 così come mostra la figura 3:



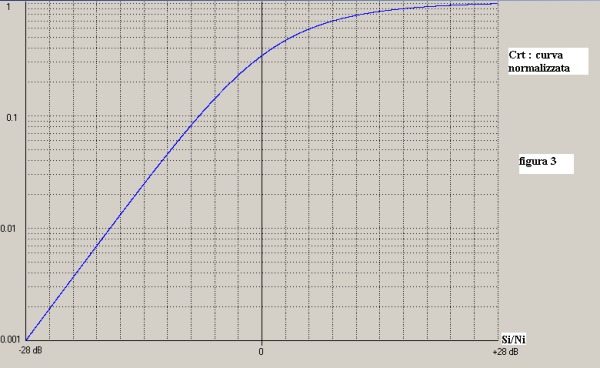
In questo grafico è ora possibile tracciare i livelli di Nux per vederne il posizionamento rispetto alla Crt; per fare questo è necessario scegliere dalla figura 2 una qualsiasi terna di valori: (F2-F1), RC, Nux con la quale tracciare sulla figura 3 una retta parallela all'asse delle ascisse con ordinata Nux.
Se ad esempio, in figura 2, si sceglie : Rc = 2 Sec. ; (F2-F1) = 2000 Hz si ha Nux = 0.0078 e la presentazione della figura 4:

3)Osservazioni sui grafici e sui numeri
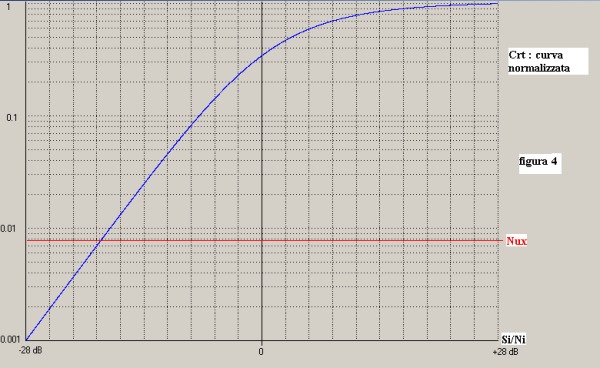
La figura 4 fornisce gli elementi per tre osservazioni:
-A) Il valore di Nux evidenziato dalla retta rossa rappresenta il massimo livello di picco che Nux, definito da RC = 2 Sec. e (F2-F1) = 2000 Hz, è in grado di provocare all'uscita del correlatore.
Il livello di Nux è relativo al massimo valore di picco; la retta non evidenzia, ovviamente, le ondulazioni casuali d'ampiezza che sono intrinseche della varianza Nux nel tempo.
Il grafico mostra che per Si/Ni > -10 dB il valore di Crt è nettamente superiore al picco di Nux con la conseguenza di avere P(D) = 100% e P(FA) = 0 per soglia posizionata sopra Nux.
Ragionevole prova di quanto affermato si può avere utilizzando la seguente formula riportata in P108 che mostra come calcolare il parametro (d) delle curve ROC dalle quali dedurre tanto P(D) che P(FA):

d = (10 ^ y) ( 2 t / BW )

dove :
il simbolo ^ indica l'elevamento a potenza
y = ( Δ + 10 Log BW ) / 5
BW = larghezza di banda dei segnali e rumori all'ingresso del correlatore (nel nostro esempio BW = F2-F1 = 2000 Hz)
t = tempo d'integrazione post correlazione (nel nostro esempio t = RC = 2 Sec.)
Δ = rapporto Si/Ni ( nel nostro esempio Si/Ni = -10 dB ) si ha:
y = (-10 dB + 10 Log 2000)/5 = 4.6
d = (10 ^ 4.6) (4 / 2000) = 79.6

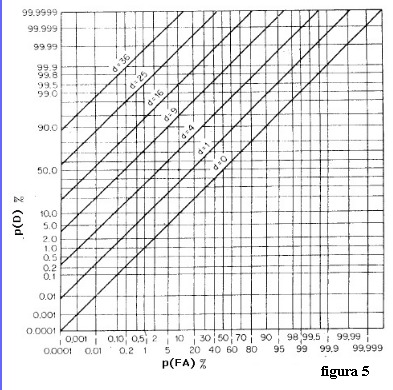
se andiamo ora a verificare sulle curve ROC, riportate in figura 5 da p80, che coppie di valori P(D) e P(FA) s'individuano, approssimativamente, per d = 79.6, nettamente al limite superiore della scala, i valori ipotizzati dall'esame di figura 4: P(D) = 100% e P(FA) = 0



-B) Il valore di Nux evidenziato dalla retta rossa rappresenta il massimo livello di picco che Nux, definito da RC = 2 Sec. e (F2-F1) = 2000 Hz, è in grado di provocare all'uscita del correlatore.
Il grafico mostra che per Si/Ni < -19 dB il valore di Crt è dell'ordine del picco di Nux con la conseguenza di avere P(D) < 100% e P(FA) > 0 per soglia tra Crt e Nux
In modo simile al primo caso scriviamo:
y = (-19 dB + 10 Log 2000)/5 = 2.8
d = (10 ^ 2.8) (4 / 2000) = 1.26

se andiamo ora a verìficare sulle curve ROC di figura 5, due coppie di valori P(D) e P(FA), tra le innumerevoli possibili, per d = 1.26 si ha:

P(D) = 50% e P(FA) = 15 %
P(D) = 90% e P(FA) = 40 %
Queste ed altre in dipendenza del diverso posizionamento della soglia di rivelazione giustificano il nostro assunto: P(D) < 100% e P(FA) > 0

-C) Il valore di Nux evidenziato dalla retta rossa rappresenta il massimo livello di picco che Nux, definito da RC = 2 Sec. e (F2-F1) = 2000 Hz, è in grado di provocare all'uscita del correlatore.
Il grafico mostra che per Si/Ni < - 25 dB il valore di Crt è nettamente inferiore al picco di Nux con la conseguenza di avere: P(D) = 0 e P(FA) = 0 se la soglia è posta sopra la retta Nux
P(D) = x% e P(FA) = x% se la soglia è posta sotto il livello di Crt
In modo simile al primo caso scriviamo:
y = (- 25 dB + 10 Log 2000)/5 = 1.6
d = (10 ^ 1.6) (4 / 2000) = 0.08

se andiamo ora a verificare sulle curve ROC di figura 5, quali coppie di valori P(D) e P(FA) sono riscontrabili per d = 0.08: ovvero sulla retta d = 0; ne segue:
P(D)è sempre uguale a P(FA) quindi, in base alla disposizione della soglia sarà sempre valido il nostro assunto:
P(D) = 0 e P(FA) = 0 se la soglia è posta sopra la retta Nux
P(D) = x% e P(FA) = x% se la soglia è posta sotto il livello di Crt

4)Un caso limite
Prendiamo ora su figura 3 una retta rappresentativa del valore di picco di Nux secondo i seguenti valori che la identificano in figura 2:
Rc = 16 Sec. ; (F2-F1) = 5000 Hz si ha Nux = 0.002 e la presentazione della figura 6:



Il valore di Nux evidenziato dalla retta rossa rappresenta il massimo livello di picco che Nux, definito da RC = 16 Sec. e (F2-F1) = 5000 Hz, è in grado di provocare all'uscita del correlatore.
Il grafico mostra che per Si/Ni = -25 dB il valore di Crt è uguale al picco di Nux con la conseguenza di avere P(D) < 100% e P(FA) > 0 per soglia inferiore a Nux
In modo simile ai casi precedenti scriviamo:
y = (-25 dB + 10 Log 5000)/5 = 2.4
d = (10 ^ 2.4) (32/ 5000) = 1.6

se andiamo ora a verìficare sulle curve ROC di figura 5, una coppia di valori P(D) e P(FA), tra le innumerevoli possibili, per d = 1.6 si ha:

P(D) = 50% e P(FA) = 10 %

Riportando ora quanto indicato in par.1.1 di p108:

Secondo le convenzioni il differenziale di riconoscimento che caratterizza un rivelatore è il minimo valore Δ per il quale si abbia:
Probabilità di falso allarme P(FA) = 10 %
Probabilità di rivelazione P(D) = 50 %