SONAR-INFO-p106

Software per il calcolo del potere di risoluzione del sonar

Funzioni attiva e passiva

1) Premessa
A completamento del lavoro presentato alle pagine p102 e p104, relativamente all'esame del potere di risoluzione angolare del sonar, esponiamo il software di calcolo utilizzato per le computazioni che in dette pagine figurano.
Compito del software è duplice:
1- trasformare una curva di direttività C(β), tracciata su carta o visualizzata su P.C. in una funzione Gaussiana sostitutiva più facilmente manipolabile per via matematica; la curva Gaussiana è sostitutiva se l'ampiezza del lobo a -3 dB è prossima a quella del lobo di C(β).
2- controllare la variazione del potere risolutivo del sonar a seguito di calibrate variazioni delle caratteristiche delle curve Gaussiane.
Non entreremo nell'ambito del listato del programma ma ci limiteremo a dettagliarne l'impiego attraverso alcuni esercizi da svolgere con apposito eseguibile, Gauss.exe, facendo ricorso a quanto illustrato sulla finzione Gaussiana nelle pagine citate.

2)Il pannello di controllo di Gauss.exe
Descriviamo il pannello di controllo secondo la figura 1:



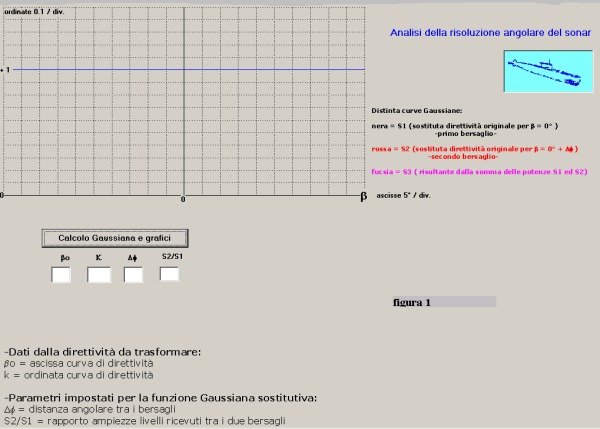
In alto a sinistra è tracciato il reticolo per la presentazione delle curve:
in ascissa 20 divisioni a da 5° ciascuna con zero centrale (variabile indipendete β).
in ordinata 15 divisioni da 0.1 ciascuna -variabile dipendente Y(β)- con asse orizzontale blu che indica il livello 1 d'ordinata

In alto a destra didascalia distintiva per le diverse funzioni tracciate che si diversificano secondo il loro colore

In basso a sinistra le caselle per l'inserimento dalle variabili di calcolo con annesso bottone di comando:
-le caselle [βo] e [ K ] sono delegate all'introduzioe dei dati ricavati dalla curva di direttività originale C(β), rispettivamente [βo] per il valore scelto dell'angolo nell'ambito della perte elevata del lobo principale e l'ordinata K corrispondente a tale angolo.
-la casella [Δ Φ] è delegata all'introduzioe del valore angolare di posizione del secondo bersaglio.
-la casella [S2/S1] è delegata all'introduzioe del rapporto tra le ampiezze dei livelli ricevuti dal sonar per S1 (primo bersaglio) e S2 (seconfo bersaglio).
-sotto la serie delle caselle dati, a seguito del calcolo, compare l'espressione esplicita della funzione Gaussiana calcolata e il valore della larghezza del suo lobo a -3 dB

3)Sulla curva di direttività C(β) che utilizzeremo ad esempio
In figura 2 è tracciata la curva di direttività dalla quale discenderanno tutte le trasformazioni e gli esempi di questa pagina:



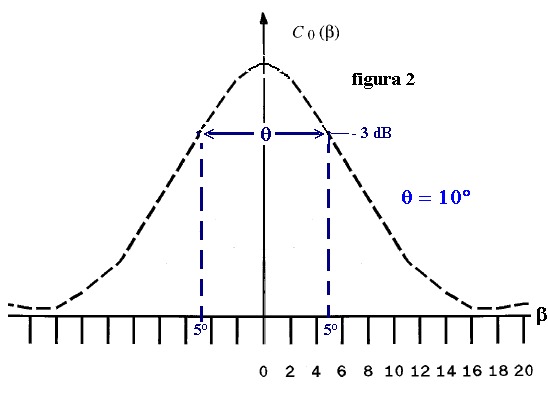
La figura mostra la larghezza del lobo principale, misurata a -3 dB, con Θ = 10°

4)La determinazione della coppia [βo] - [ K ] di C(β)
L'analisi del potere risolutivo angolare del sonar deve iniziare con l'osservazione della caratteristica di direttività originale C(β), sia questa evidenziata su tracciato su carta, sia definita con adatto algoritmo su video di P.C.
Supponiamo che il tracciato della curva di direttività sia quello ridotto di figura 2 e mostrato in figura 3:



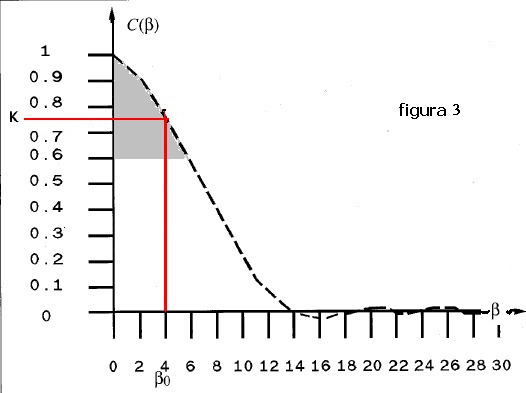
Dalla figura devono essere estratti i valori della coppia di coordinate [βo] - [ K ] da scegliere nella parte alta del lobo di direttività, zona grigia, ragionevolmente attorno ad un valore di K pari a 0.7 (larghezza del lobo a - 3dB), nella figura 3 possiamo sceglire, come indicato in rosso, la coppia k = 0.74 ; βo = 4°.
I valori sopra indicati devono essere inseriti nelle apposite caselle del pannello di controllo.
Se le successive operazioni lo riciederanno si dovrà ripetere la procedura per sceglire una coppia di coordinate in una diversa posizione rispetto a questa.

5)La definizione della distanza angolare tra i due bersagli e la loro pressione acustica
Il valore della distanza angolare tra i due bersagli deve essere impostato secondo la definizione:
"con buona approssimazione, la risoluzione angolare Δφ è identificabile con la larghezza, a -3dB, del lobo di direttività di C(β)"
Con riferimento a figura 2, essendo Θ = 10° si ha : Δφ = 10°
I livelli di pressione acustica ricevuti dalla base del sonar devono essere impostati, nella prima fase di calcolo, con S1 = 1 e S2 = 1 ( S2/S1 = 1).
Tanto Δφ che S2/S1 devono essere digitati nelle apposite caselle del pannello di controllo di figura 1.

6)La prima fase di calcolo
Una volta inserite, nel pannello di controllo, le quattro varabili :
k = 0.74 ; βo = 4°
Δφ = 10° ; S2/S1 = 1
a seguito della pressione del bottone "Calcolo della Gaussiana e grafici" si ha la presentazione completa di figura 4:



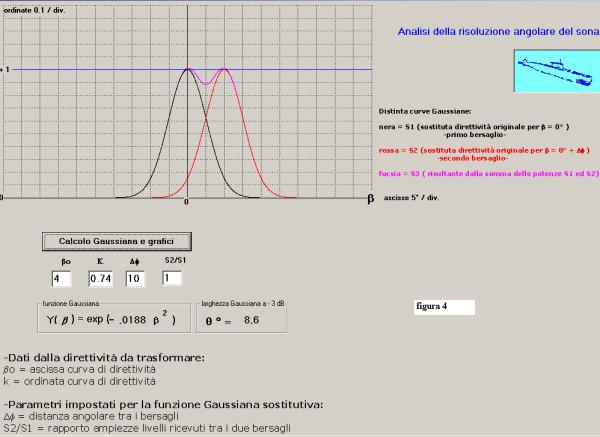
In figura osserviamo:
- la funzione esplicita y(β) sostitutiva di C(β)
y(β) = exp (-0.0188 β²)
- la larghezza a - 3 dB del lobo di y(β) pari a Θ = 8.6°
- la curva Gaussiana S1 tracciata con S1 = 1 per la direzione 0° -colore nero-
- la curva Gaussiana S2 tracciata con S2 = 1 per la direzione 0° + 10° -colore rosso-
- la curva a sella dovuta alla somma delle potenze di S1 e S2 -colore fucsia-
Le seguenti osservazioni sono necessarie:
A)-il valore Θ = 8.6° è un poco diverso da Θ = 10°, approssimazione sufficiente per il lavoro da svolgere in questa pagina; eventuali maggiori precisioni richieste possono essere ricercate per diverse coppie k ; βo .
B)-la distanza tra i massimi delle due curve Gaussiane è pari al valore introdotto di Δφ = 10°.
C)-la curva a sella presenta i due massimi, leggermente spostati angolarmente rispetto ai massimi delle Gaussiane per effetto dell'interferenza reciproca fra le due nell'operazione di somma.
D)-l'ampiezza della sella è circa 0.1 in conformità con la definizione di potere risolutivo angolare.

6)La variazione del potere risolutivo angolare al variare di S2 o di S1
La variazione del potere risolutivo angolare si evidenzia con la modificazione del rapporto S2/S1 a seguito, ad esempio, della riduzione d'ampiezza di S2; detta riduzione può essere attribuita fisicamente a riduzione della velocità del bersaglio o ad allontanamento dello stesso rispetto alla base del sonar.
Per esaminare una casistica di condizioni, a parità di identiche variabili k = 0.74 ; βo = 4° ; Δφ = 10° ; assumiamo per il rapporto S2/S1 i seguenti valori:
1 ; 0.8; 0.6; 0.4; 0.2: per ciascun rapporto tracciamo il grafico sul pannello di controllo.
Per ridurre l'ingombro di 5 figure riportiamo soltanto per ciascuna parte del reticolo così come in figura 5:



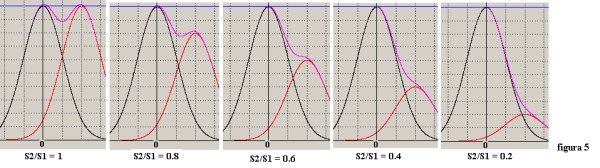
Le curve di figura 5 sono così descritte:
-curva S2/S1 = 1 : curva originale già riportata in figura 4 ; ampiezza sella = 0.1 (risoluzione ottimale)
-curva S2/S1 = 0.8 : ampiezza sella = 0.04 (risoluzione al limite)
-curva S2/S1 = 0.6 : ampiezza sella = 0.01 (risoluzione incerta)
-curva S2/S1 = 0.4 : ampiezza sella = 0.01 (risoluzione impossibile)
-curva S2/S1 = 0.2 : ampiezza sella = 0 (risoluzione impossibile)
Ciò a dimostrazione della decadenza del potere risolutivo del sonar al ridursi di un segnale di bersaglio rispetto all'altro.

7)Ricerca del potere risolutivo del sonar per S2/S1 diverso da 1
Con Gauss.exe è possibile trovare il potere risolutivo del sonar in condizioni di S2/S1 < 1 affidandoci alla ricerca di una curva S3 con sella dell'ordine di 0.1.
Se ad esempio si osserva la curva S2/S1 = 0.4 indicata nel paragrafo predente e con tale rapporto S2/S1 si ripetono i calcoli variando di volta in volta a crescere il valore di Δφ troviamo il ripristinarsi della sella d'ampiezza 0.1 per Δφ = 15° così come mostra la figura 6:



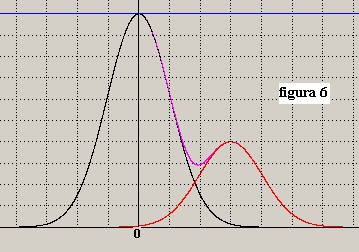
L'esempio indica che una riduzione del rapporto S2/S1 a 0.4 deteriora il potere risolutivo del sonar che passa da 10° a 15°.

8)Conclusioni
L'impiego di Gauss.exe, il cui eseguibile è qui disponibile: Gaussdir, consente un'analisi veloce di tutte le problematiche legate alla risoluzione angolare delle curve di direttività dei sonar in fase di studio preliminare o di presa d'atto di condizioni da verificare sul campo.