Geometria analitica (1°) - relazione tra punti e rette -
Richiami per lo studio delle basi idrofoniche

1)Generalità
Nello studio delle caratteristiche di direttività delle basi acustiche dei sonar si ricorre, sovente, agli algoritmi della geometria analitica per il calcolo delle coordinate di posizione dei singoli idrofoni che ne costituiscono la struttura ricevente.
Un esempio di questa tecnica è mostrato in p20, p22, per lo studio delle basi idrofoniche utilizzabili dal sonar FALCON nell'ipotesi d'impiego sui battelli U212.
In p22 in particolare è disponibile un file.exe (file applicativo), compilato con algoritmi di geometria analitica, con il quale scegliere la posizione ottimale dei sensori acustici sulla struttura conforme già in sede operativa.
In questi casi l'impiego di file.exe si è dimostrato utile è veloce per la ricerca delle diverse combinazioni di posizione tra la consistente serie di sensori disponibili; da ciò scaturisce l'idea di fornire una serie di file eseguibili, ciascuno indirizzato a diversi algoritmi di geometria analitica, con i quali prendere confidenza all'impiego degli algoritmi stessi, dai più semplici ai più complessi, estrapolabili per la soluzione di problematiche relative all'analisi delle basi acustiche dei sonar.
Una premessa è necessaria prima del prosieguo della pagina: gli algoritmi utilizzati non sono dimostrati per via matematica ma soltanto implementati, a favore del calcolo automatico, in apposite routine in Visual Basic; per le dimostrazioni si rimanda agli innumerevoli testi di geometria analitica in commercio.

2)La relazione tra i punti e le rette
Uno tra i più semplici problemi di geometria analitica riguarda la relazione tra i punti tracciati nel piano cartesiano e le rette che possono intercettarli; un file applicativo per la soluzione grafica e numerica di uno tra gli innumerevoli proponibili è disponibile cliccando su (zip) .

Gli algoritmi implementati in (eserc.PR), scritti in linguaggio V.B. sono:

-coordinate singoli punti : (x1; y1) , (x2; y2) , ....(xn; yn)

-distanza tra due punti: dist23 = Sqr((X2 - X3) ^ 2 + (Y2 - Y3) ^ 2)

-area del triangolo formato da tre punti:
p = (dist12 + dist13 + dist23) / 2
Area = Sqr(p * (p - dist12) * (p - dist13) * (p - dist23))

-equazione retta generica passante per due punti P(X1;Y1) - P(X2;Y2):
m = (Y2 - Y1) / (X2 - X1)
n = Y1 - m * X1
Y = m * X + n

-retta perpendicolare ad una retta data: Y = m * X + n ---> Y = (-1 / m) * X + n

3)Esempio d'impiego di eserc.PR
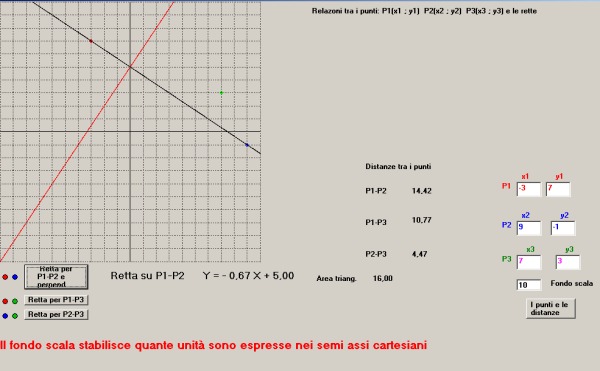
Stabilite e digitate le coordinate dei tre punti e il valore di fondo scala:
P1(-3 ; 7) _ P2(9 ; -1) _ P3(7 : 3)
fondo scala = 10 (pari a 1 unità / divisione)
si ha:
-premendo il pulsante "I punti e le distanze" la comparsa nel reticolo dei 3 punti, diversamente colorati ( rosso - blu - verde ), e i segmenti che ne identificano le distanze relative.
Compaiono inoltre i valori delle distanze calcolate e l'area del triangolo compreso tra i 3 punti.
dist.P1-P2 = 14.42
dist.P1-P3 = 10.77
dist.P2-P3 = 4.47
Area triangolo = 16.00
Premendo successivamente i pulsanti "Retta per .." compaiono le rette passanti per i punti dati; per la prima, nell'ordine, anche la sua perpendicolare.
Per ciascuna retta, ad esclusione della perpendicolare alla prima, ne viene visualizzata l'equazione con i valori di "m" ed "n" espressi con numeri decimali.
Per la retta passante per P1-P2 l'equazione risultante è : Y = - 0.67 X + 5
Si deve osservare che il tracciamento di rette parallele all'asse Y non è fattibile su P.C. essendo "m" = ∞ , nel caso che i calcoli portino a tale condizione le rette non vengono presentate sullo schermo.
La schermata risultante è visibile nella figura seguente: