SONAR-INFO-p123
Gli integrali delle funzioni iperboliche
-Sviluppi analitici degli integrali indefiniti -
-Calcolo automatico del valore numerico tra i limiti d'integrazione per gli integrali definiti-
Il calcolo del valore numerico degli integrali definiti delle funzioni iperboliche non sempre si presta ad essere affrontato in modo semplice; in alcuni testi di matematica applicata sono disponibili numerose tabelle con le quali Ŕ possibile ricavare il valore degli integrali definiti in particolari campi di variabilitÓ degli estremi d'integrazione.
Il problema accennato Ŕ risolvibile, per un numero limitato di funzioni, tramite un particolare file.exe ( INTEGRALMATH-ipb- ) che consente il calcolo rapido del valore numerico dell'integrale definito prescelto dall'operatore.
Nelle tabelle citate i valori numerici sono definiti con un numero di cifre generalmente molto elevato, da 4 a 10, nella routine di INTEGRALMATH-ipb- la precisione Ŕ limitata a 5 decimali.
2) Le funzioni iperboliche disponibili
La raccolta delle funzioni disponibili nel file eseguibile Ŕ mostrata nella figura 1, senza alcun ordine, ne di complessitÓ, ne di importanza, indicandone l'espressione esplicita e a fianco ad essa l'espressione dell'integrale indefinito appositamente sviluppato:
 figura 1
figura 1 Per ciascuna delle 8 funzioni iperboliche Ŕ disponibile, tramite il pulsante di "selezione e calcoli" di "INTEGRALMATH-ipb-" mostrato in figura 1 la sezione applicativa con la schermata di lavoro visibile in figura 2:
 figura 2
figura 23) Esempio d'impiego di INTEGRALMATH-ipb-
Una volta lanciato l'eseguibile si ha la presentazione della prima pagina cosý come mostrato in figura 1, dall'elenco delle 8 funzioni si pu˛ copiare l'integrale indefinito della funzione iperbolica interessata, supponiamo sia la n░ 7 che trascriviamo:
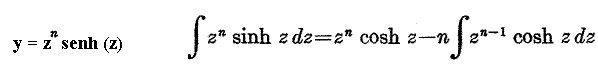
Se ora si vuole calcolare l'integrale definito della funzione prescelta si agisce sul pulsante "Selezione e calcoli" per passare alla pagina di lavoro di figura 2.
Per selezionare la 7, si clicca sul 7░ bottone di selezione, si digitano negli appositi spazi i limiti d'integrazione, supponiamo z1 = 2 ; z2 = 3 ; n = 2 pigiando il pulsante "Calcolo" si ha la comparsa, nell'apposito label celeste, del valore dell'integrale definito che, come si vede da figura 2 Ŕ; I = 42.56981
Data la complessitÓ di elaborazione il valore dell'integrale definito non compare immediatamente nel label celeste ma necessita di un certo tempo d'attesa.
Il tempo Ŕ subordinato, sia dai valori di z1; z2; n; messi a calcolo; sia dalla complessitÓ della funzione logaritmica prescelta, sia infine dalla velocitÓ de P.C.